Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 14.4 - Ex. 3
Calcule se a resposta é . Use o resultado para calcular a resposta forçada, se .
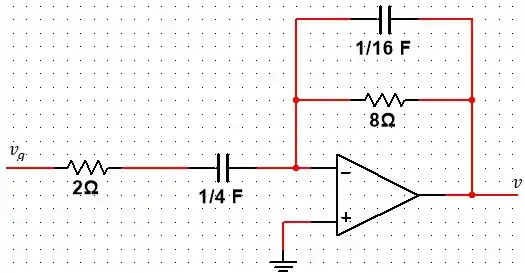
Passo 1
Falaeee, beleza??? Essa aqui é beleza demais!! Se ligaaa!!
Sabemos que, para uma resistência , a impedância é:
Para uma indutância , sua impedância é:
E, para uma capacitância , sua impedância é:
Nesse sentido, para o circuito desse exercício (e já colocando os sentidos das correntes), temos:
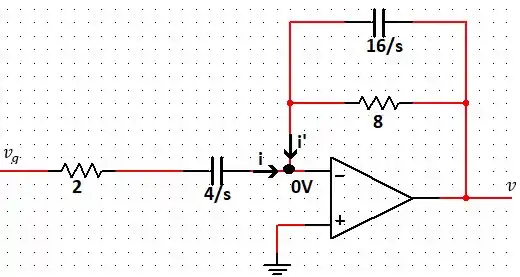
Passo 2
Analisando o circuito, podemos perceber que:
Além disso, também percebemos que:
Ademais, temos que:
Logo, temos que:
Assim, concluímos que:
Passo 3
Calculando a resposta forçada, temos que:
Substituindo valores e sabendo que , temos:
Ou seja:
Resposta
Exercícios de Livros Relacionados
Calcule a corrente i em regime permanente, se i g = 9 - 20 cos t - 39 cos 2 t + 18 cos 3 tA .
Demonstre qu Y = Y 1 + 1 Z 2 + 1 Y 3 + 1 Z 4 + 1 Y 5 (Sugestão: Observe que Y = Y 1 + Y a = Y 1 + 1 / Z a = Y 1 + 1 / ( Z 2 + Z b ) = … )
Calcule v ( t ) , se (a) V ( s ) = 6 ∠ 10 ∘ com s = - 2 + j 8 ; (b) V ( s ) = 5 ∠ 0 ∘ c o m s = - 10 ; (c) V ( s ) = 4 + j 3 com s = - 1 + j 2 e (d) V ( s ) = - j 6 com s = j 4 .
Calcule a impedância Z ( s ) vista pela fonte e coloque seus pólos e zeros. Se a fonte é v g = 10 e - 2 i c o s 4 t V , calcule a componente forçada da corrente que ela entrega
Use o princípio da proporcionalidade para calcular a função de rede V 2 V 1 e use o resultado para calcular a resposta forçada v 2 ( t ) , quando v 1 ( t ) = 4 c o s tV