Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 11.Problemas - Ex. 25

Calcule a tensão v em regime permanente, se v_g = 3 cos 2 t V .

Passo 1

Falaeeee meu consagrado, bora resolver mais uma de amp op? Vem comigo haha

Bora continuar com aquele padrãozinho... Primeiro vamos analisar o circuito com os capacitores em forma de reatâncias e colocar v_g na forma polar.

Lembrando que:

X_C = - (j)/(omega C)

Em que omega = 2 r a d // s .

Logo, temos:

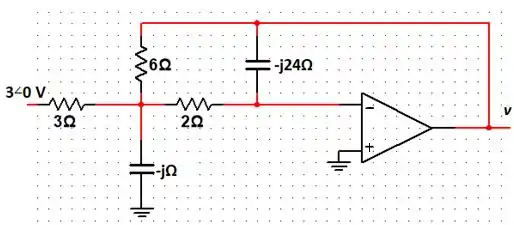
Passo 2

Se vc reparar, a entrada inversora está diretamente conectada ao terra, ou seja, tem potencial 0V. Isso quer dizer que a tensão em ambas as entradas são 0V!!

Nesse sentido, vamos selecionar os nós e atribuir direções da corrente aqui para podermos analisar melhor a situação:

Passo 3

Analisando o seguinte ramo, temos que:

(v 1)/(2) + (v)/(- j 24) = 0 :.

j v + 12 v 1 = 0

Passo 4

Agora, aplicando LKC no nó v 1 para o circuito completo, temos:

(3 - v 1)/(3) + (v - v 1)/(6) = (v 1)/(- j) + (v 1)/(2) :.

1 - (v 1)/(3) + (v)/(6) - (v 1)/(6) = j v 1 + (v 1)/(2) :.

Multiplicando a equação por 6, temos:

6 - 2 v 1 + v - v 1 = j 6 v 1 + 3 v 1 :.

v + v 1 (- 6 - j 6) = - 6

Passo 5

Assim, temos o seguinte sistema:

{[[j v + 12 v 1 = 0],[v (j) + v 1 (6 - j 6) = - j 6]])

Resolvendo o sistema pela Regra de Cramer para o sistema 2x2, temos que v é:

v = (|[[0,12],[-,j,6,6,-,j,6]]|)/(|[[j,12],[j,6,-,j,6]]|) :.

v = (- j 72)/(6 - j 6) :.

v = 6 sqrt(2) /_ 135 ° V

Tranquilinho??? Valeeeu!!

Resposta

v = 6 sqrt(2) cos (2 t + 135 °) V

Exercícios de Livros Relacionados

A fonte de tensão senoidal no circuito visto na Figura P9.77 está funcionando a umafrequência de 200 krad/s. O coeficiente de acoplamento é ajustado até que o valor de pico de i1 seja máximo.a) Qual é
a) Determine as expressões de regime permanente para as correntes ig e iL no circuito daFigura P9.76, quando vg = 168 cos 800t V.b) Determine o coeficiente de acoplamento.c) Determine a energia armaze
Como engenheiro formado, pode ser que você tenha a oportunidade de trabalhar como perito em ações judiciais que envolvam danos à propriedade ou a pessoas. Como um exemplo desse tipo de problema, para