Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 2.Problemas - Ex. 67
67.
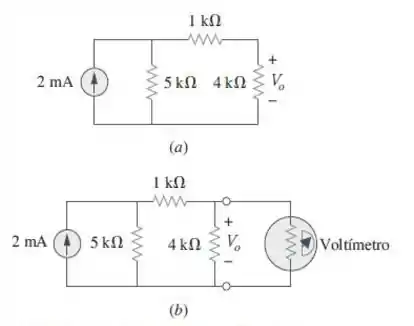
(a) Calcule a tensão no circuito da figura
(b) Determine a tensão medida quando um voltímetro com resistência interna de estiver conectado conforme mostrado na figura
(c) A resistência finita do medidor introduz um erro na medida. Calcule o erro percentual como
(d) Determine o erro percentual caso a resistência interna fosse de .
Passo 1
a) Bom! A primeira coisa que temos de fazer é destacar algumas partes importantes de nosso circuito! Vamos lá!
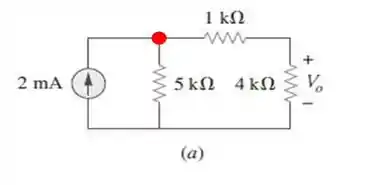
Viu só essa ponto vermelho. Assim que a corrente de chega nele, ela se divide um duas partes. Acontece que os dois ramos tem a mesma resistência total, uma de e o outro ramos contém duas resistências em série, uma de e outra de , o que dá . Assim por divisão de corrente, temos que a corrente circulante no resitor de , é:
E para obter o valor de , basta multiplicar essa corrente pelo valor da resistência, no caso de .
Passo 2
b) O voltímetro com resistência interna de está em paralelo com aquela resistência interna de . Sendo assim, a resistência equivalente dessa associação vale:
E como estamos trabalhando com um circuito em paralelo, onde os ramos tem a mesma tensão; vamos descobrir o valor da corrente circulante. Sendo assim, por divisão de corrente, obtemos o seguinte valor:
Obtemos desse jeito, que a tensão vale:
Passo 3
c) Nessa letra, para descobrir o valor do erro em função da introdução da resistência finita, basta usar a fórmula a seguir, substituindo os valores que já obtivemos dos e :
Passo 4
d) Nesse caso, o voltímetro tem uma resistência interna de que está em paralelo com aquela resistência interna de . Sendo assim, a resistência equivalente dessa associação vale:
E como estamos trabalhando com um circuito em paralelo, onde os ramos tem a mesma tensão; vamos descobrir o valor da corrente circulante. Sendo assim, por divisão de corrente, obtemos o seguinte valor:
Obtemos desse jeito, que a tensão vale:
De modo que o nosso erro, passa a ser então:
Resposta
a)
b)