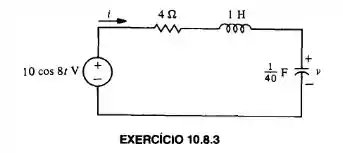
Calcule , a tensão em regime permanente no Ex. 10.8.3, usando fasores e divisão de tensão.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Primeiro, vamos fazer as conversões para fasores, então, temos o seguinte
O resistor fica com a mesma resistência, logo temos o seguinte circuito
Passo 2
O problema nos pediu para fazer um divisor de tensão, então vamos considerar o termo como uma resistência equivalente, com isso, nós temos que
Transformando para fasores, nós temos que
Voltando para o domínio do tempo, nós obtemos que