Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 9.Problemas - Ex. 84

Uma carga equilibrada, ligada em Y, tem uma impedância de 60 - j45 Ω / ϕ e está ligada em

paralelo com uma carga equilibrada, ligada em ∆ , cuja impedância é 90 2 / 45 °   Ω / ϕ . As

cargas em paralelo são alimentadas por uma linha com uma impedância de 2 + j2 Ω / ϕ . O

módulo da tensão fase-fase da carga em ∆ é 300 3 V.

  1. Calcule o módulo da corrente de fase na carga ligada em Y.
  2. Calcule o módulo da corrente de fase na carga ligada em D.
  3. Calcule o módulo da corrente na linha que alimenta as cargas.
  4. Calcule o módulo da tensão de linha no início dela.

Passo 1

Falaaa, pessoal! Como vocês estão?

Bora pra mais uma questãozinha pra exercitar o que a gente sabe circuitos trifásicos equilibrados!

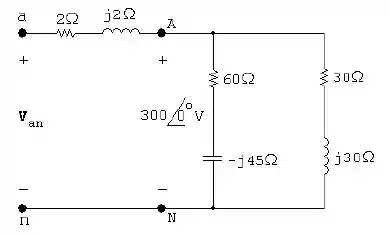
  1. Começamos ilustrando o sistema:

    2. Feito isso, podemos determinar a corrente na linha aA e seu módulo:

    I a A = 300 60 - j 45 + 300 30 + j 30 = 8,6 / - 17,59 ° A

    I a A = 8,6 A

    Passo 2

    De forma similar, vamos fazer isso pra todas as correntes em linha:

  2. Linha AB:

    3. I A B = 300 3 / 30 ° 90 + j 90 = 4,08 / - 15 ° A

    I A B = 4,08 A

  3. Linha AN:

    4. I A N = 300 / 0 ° 60 - j 45 = 4 / 36,87 ° A

    I A N = 4   A

  4. Calculando o módulo da tensão de linha no início:

V a n = ( 8,6 / - 17,59 ° ) ( 2 + j 2 ) + 300 / 0 ° = 321,79 / 1,99 ° V

V a n = 557,37   V

Resposta

  1. Item a:

    2. I a A = 8,6 A

  2. Item b:

    3. I A B = 4,08 A

  3. Item c:

    4. I A N = 4   A

  4. Item d:

V a n = 557,37   V

Exercícios de Livros Relacionados

Calcule as frequências naturais do circuito da Fig. 14.5 matando as fontes e usando (a) uma entrada de alicate em serie com 0 capacitor e (b) uma entrada de soldagem através do capacitor.
Um filtro passa-todas é o filtro cuja resposta em amplitude e constante. (Então, ele passa todas as frequências igualmente bem). Pode ser Iigado em cascata com outro filtro par manter uma resposta em
Para o circuito RLC paralelo em ressonância, mostre que a energia total armazenada é w t = 1 2 R 2 C I M 2 cos 2 ⁡ w 0 t + R 2 I M 2 2 w 0 2 L sin 2 ⁡ w 0 L = 1 2 R 2 C I M 2 Onde a excitação é i = I
No Ex. 14.4.3, substitua 0 resistor de 8Ω por 2Ω , mostre que o circuito e um filtro passa-faixa e caIcule w oeQ .
Para o circuito RLC serie com excitação v g = v m cos ⁡ w tV , mostre que w 0 = 1 L C e Q = w 0 L R . A resposta é corrente de laço.