Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 10.4 - Ex. 4

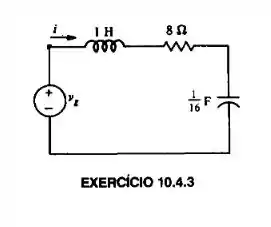
Repita o Ex. 10.4.3, se v_g = 16 cos 4 t V

Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

Essa questão tem o mesmo raciocínio da 10.4.3, logo já conhecemos o algoritmo, então vamos lá, primeiramente, EDO, temos que

L (d^2 i)/(d t^2) + R (d i)/(d t) + (1)/(C) i = 64 j e^(j 4 t)

Já com os termos convertidos para exponenciais, logo, substituindo os valores, nós temos que

(d^2 i)/(d t^2) + 8 (d i)/(d t) + 16 i = 64 j e^(j 4 t)

Agora, podemos brincar um pouco mais com essa EDO.

Passo 2

Substituindo nosso palpite i = A e^(j 4 t) , temos que

(- 16 + 32 j + 16) A e^(j 4 t) = 64 j e^(j 4 t)

Logo, A será igual a

A = (64 j)/(32 j) = (64 /_ 90 °)/(32 /_ 90 °) = 2 /_ 0 °

Convertendo para o domínio do tempo, nós temos que

i (t) = 2 cos 4 t A

Resposta

i (t) = 2 cos 4 t A

Exercícios de Livros Relacionados

Calcule as frequências naturais do circuito do Ex. 14.4.2 matando a fonte e usando (a) uma entrada de alicate em serie com 0 capacitor e (b) uma entrada de soldagem através do capacitor. (Nota: não ca
Calcule as frequências naturais do circuito da Fig. 14.5 matando as fontes e usando (a) uma entrada de alicate em serie com 0 capacitor e (b) uma entrada de soldagem através do capacitor.
Um filtro passa-todas é o filtro cuja resposta em amplitude e constante. (Então, ele passa todas as frequências igualmente bem). Pode ser Iigado em cascata com outro filtro par manter uma resposta em
Para o circuito RLC paralelo em ressonância, mostre que a energia total armazenada é w t = 1 2 R 2 C I M 2 cos 2 ⁡ w 0 t + R 2 I M 2 2 w 0 2 L sin 2 ⁡ w 0 L = 1 2 R 2 C I M 2 Onde a excitação é i = I
No Ex. 14.4.3, substitua 0 resistor de 8Ω por 2Ω , mostre que o circuito e um filtro passa-faixa e caIcule w oeQ .