Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 11.Problemas - Ex. 24

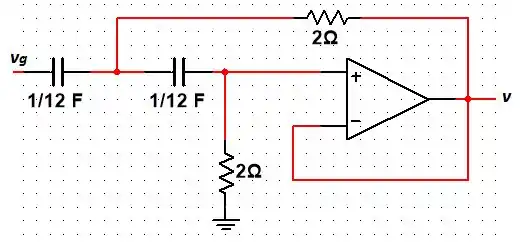
Calcule a tensão v em regime permanente, se v_g = 5 cos 3 t V .

Passo 1

Mais uma de Amp Op ein?! Bebe um golinho de água e vamos juntos!!

Bora continuar com aquele padrãozinho... Primeiro vamos analisar o circuito com os capacitores em forma de reatâncias e colocar v_g na forma polar.

Lembrando que:

X_C = - (j)/(omega C)

Em que omega = 3 r a d // s .

Logo, temos:

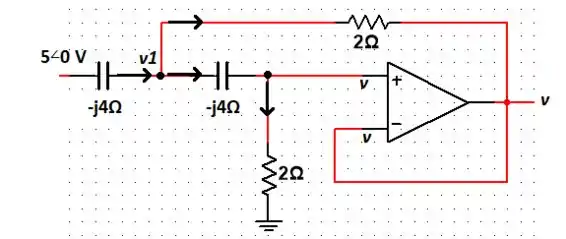
Passo 2

Se vc reparar, a entrada inversora está diretamente conectada (curto circuitada) com a saída do Amp Op. Isso quer dizer que a tensão em ambas as entradas são v !! Isso facilita muito!

Nesse sentido, vamos selecionar os nós e atribuir direções da corrente aqui para podermos analisar melhor a situação:

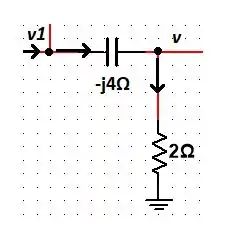
Passo 3

Analisando o seguinte ramo, temos que:

(v 1 - v)/(- j 4) = (v)/(2) :.

v (- 2 + j 4) + 2 v 1 = 0

Passo 4

Agora, aplicando LKC no nó v 1 para o circuito completo, temos:

(5 /_ 0 ° - v 1)/(- j 4) = (v 1 - v)/(- j 4) + (v 1 - v)/(2) :.

v (- 1 + j 2) + v 1 (2 - j 2) = 5

Passo 5

Assim, temos o seguinte sistema:

{[[v (- 2 + j 4) + 2 v 1 = 0],[v (- 1 + j 2) + v 1 (2 - j 2) = 5]])

Resolvendo o sistema pela Regra de Cramer para o sistema 2x2, temos que v é:

v = (|[[0,2],[5,2,-,j,2]]|)/(|[[-,2,+,j,4,2],[-,1,+,j,2,2,-,j,2]]|) :.

v = (10 /_ 0 °)/(- 6 - j 8) :.

v = 1 /_ 126.87 ° V

E vamo que vamo pra outra questãozinha!!

Resposta

v = 1 cos (3 t + 126.87 °) V

Exercícios de Livros Relacionados

26. Utilize a análise de malhas para determinar i 0 no circuito da Figura 10.74
27. Usando a análise de malhas, determine I 1 e I 2 no circuito da figura 10.75
28. No circuito da Figura 10.76 , determine as correntes de malha i 1 e i 2 . Seja v 1 = 10 cos ⁡ 4 tV e v 2 = 20 cos ⁡ ( 4 t - 30 ° ) .
29. Utilizando a figura 10.77 , elabore um problema para ajudar outros estudantes a entenderem melhor a análise de malhas.
30. Use a análise de malhas para determinar v 0 no circuito da figura 10.78 . Seja v s 1 = 120 cos ⁡ ( 100 t + 90 ° )V e v s 2 = 80 cos ⁡ ( 100 t )V .