Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 11.Problemas - Ex. 27
Calcule o valor de em regime permanente.
Passo 1
Uepaaaa!! Quequeiiiisssso?! O.O
Brincadeira brincadeira, é a mesma coisa que a gente tava fazendo antes ;p
Seguinte... Vamos primeiro passar os valores das fontes para a forma polar e enxergar o capacitor e os indutores em forma de reatâncias.
Lembrando que:
Em que .
Logo, temos:
Passo 2
Podemos descobrir o valor de aplicando o teorema da superposição. Vc faz primeiro a corrente do circuito somente abastecido pela fonte de (tratando a fonte de tensão como curto circuito) e depois faz a mesma coisa somente com a fonte de (tratando a fonte de corrente como circuito aberto). Aí por fim a gente soma os dois valores de tensão!!
Ficou confuso?? Então vem aqui ;)
Primeiro vamos fazer com a fonte de :
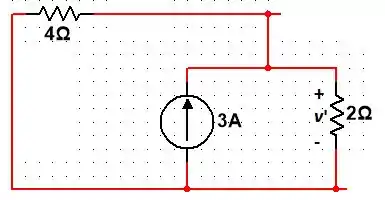
Note que, por se tratar de uma fonte de corrente contínua, vale lembrar que:
- Capacitores são vistos como circuitos abertos;
- Indutores são vistos como curto circuitos.
Pelo divisor de corrente, a corrente no resistor de é dada por:
Logo, pela Lei de Ohm, a tensão no resistor de é dada por:
Aí foi simplesinho né? Haha
Passo 3
Agora, para a fonte de :
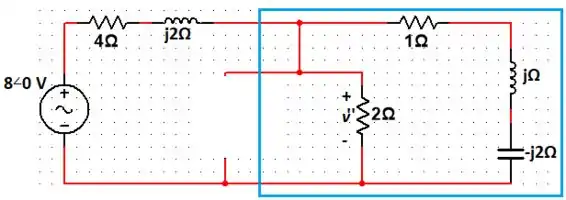
Vamos descobrir a impedância equivalente dentro daquele retângulo azul e aí depois é só fazer o divisor de tensão (pois a tensão em cima dessa impedância é a mesma que ). Entendeu o macete? haha
Fazendo o divisor de tensão
Passo 4
Por fim, somando as duas tensões, temos:
Viu como é fácil? Vaaaamos prosseguir com mais questõezinhas!!