Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 16.Problemas - Ex. 14

Calcule no transformador da Fig. 16.3(a), quando i 1 = 2   A e i 2 = 4   A , se L 1 = 2 H , L 2 = 10 H e M = 4 H . (b) Repita a parte (a), se um dos pontos de polaridade for passado para o outro terminal.

Passo 1

E aí gurizada tudo belezinha?

Vem comigo para mais um exercício :😉

10 ∠ 0 ∘ = ( 2 + j 5 ) I 1 - j 4 I 2

0 = - j 4 I 1 + ( 1 + j 10 ) I 2 + j 4 I 3

0 = j 4 I 2 + ( 2 + j 4 ) I 3

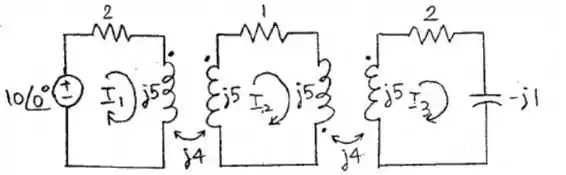
Da malha 1 e malha 2

( 1 + j 10 ) 10 ∠ 0 ∘ = - 32 + j 25 I 1 - 16 I 3

Passo 2

Da malha 2 e malha 3

0 = 16 I 1 + ( 22 - j 24 ) I 3

I 1 = ( 1 + j 10 ) 10 - 16 0 22 - j 24 - 32 + j 25 - 16 16 22 - j 24 = 2.47 ∠ - 46.6 ° ⋅ A

I 3 = - 32 + j 25 10 ( 1 + j , 0 ) 16 0 - 32 + j 25 - 16 16 22 - j 24

1.21 ∠ - 179.1 ° A

Resposta

1.21 ∠ - 179.1 °   A

Exercícios de Livros Relacionados

Repita o Prob. 16.6
Se L 1 = 4 H , L 2 = 3 H , M = 2 H e as correntes i 1 e i 2 estāo variando com uma taxa de variaçāo de - 2A / s e 10A / s , respectivamente, calcule v 2 e v 2 e m (a) Fig. 16.3(a) e (b) Fig. 16.3 (b).
Calcule v ( t ) , para t0 , usando (a) análise de laço e (b) análise nodal.
Note que, para bobinas acopladas, podemos sempre escolher as atribuições de corrente entrando nos pontos e as polaridades positivas das tensões nos pontos, como na Fig. 16.3(a). (Isso, certamente, pod
Calcule M , se L 1 = 0,4 H , L 2 = 0,9 H