Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 5.Problemas - Ex. 31

Calcule i usando transformações de fontes para obter o circuito equivalente no que se relaciona ao resistor de 1KΩ, contendo uma fonte e um resistor, além do resistor de 1KΩ.

Passo 1

Falaaa, galerinha!!! Vamos mandar ver nessa questão 😉.

Dá uma olhadinha no circuito. Ele quer que achemos a corrente do resistor de 1KΩ e faça equivalente de Thévenin menos do resistor de 1KΩ então iremos mantê-lo intacto. Agora, que já sabemos o que a questão nos pede, vamos mandar bronca!

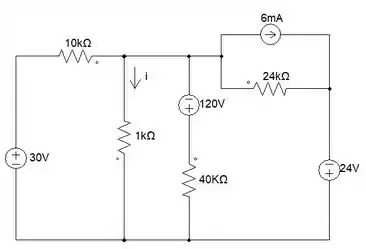
Antes de tudo, precisamos saber o nosso R t h e para isso, precisamos reduzir um pouquinho nosso circuito fazendo algumas transformações de fontes, a fim de, podermos manipulá-las. Então, capitou aí?

Vamos analisar beeem direitinho. Percebeu que o resistor de 24KΩ está em paralelo com uma fonte de corrente? Isso significa que podemos fazer lei de Ohm e transformar para uma fonte de tensão em série. Vamos lá 💪

V 1 =   R 24 ⋅ i 6

V 1 =   24 k ⋅ 6 m

V 1 =   144 V

Boa, pessoal!! Vamos analisar o circuito mais um pouquinho. Viu que que o resistor de 40KΩ está em série com a fonte de tensão de 120V? Isso significa que podemos fazer lei de Ohm e transformar para uma fonte de corrente em paralelo. Vamos lá 💪

i 1 = V 120 R 40

i 1 = 120 40 K

i 1 = 3 m A

Passo 2

Muito bem, galaerinha! Feito isso, vamos ver como ficou o circuito com essas transformações.

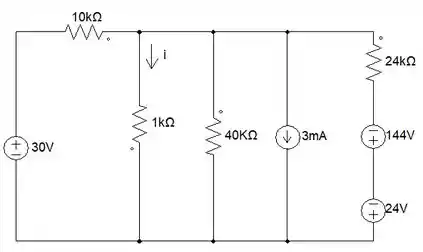
Ainda não está do jeito que queremos. Vamos ver o que podemos fazer agora🤔. Percebeu que tem duas fontes de tensão em série? Tu tira onda mesmo! Vamos fazer o equivalente delas.

V 2 = V 24 + V 144

V 2 = 24 + 144

V 2 = 168 V

Aí sim! Agora, como o V 2 ficou em série com o resistor de 24KΩ, iremos transformar para uma fonte de corrente em paralelo. Partiu!

i 2 = V 168 R 24

i 2 = 168 24 K

i 2 = 7 m A

Essa fonte terá o sentido para baixo, logo ela será negativa.

i 2 = - 7 m A

Massa, pessoal. Está indo muito bem! Agora, ficaremos com duas fontes de corrente em paralelo, assim, podemos juntá-las e ficarmos com uma equivalente. Bora lá!

i e q = - i 2 - i 1

i e q = - 7 - 3

i e q = 10 m A

Passo 3

Show de bola!!! 😍 Olha aí como vai ficar nosso circuito agora:

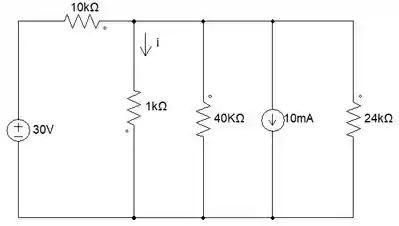
Beleza, pessoal. Ainda dá para fazermos mais uma transformação de fonte com o resistor de 10KΩ e a fonte de tensão. Vai ficar assim:

i 3 = V 30 R 10

i 3 = 30 10 K

i 3 = 3 m A

Maravilha! Com essa transformação, teremos 3 resistores em paralelo, lembrando que não estamos usando o resistor de 4Ω ainda. Vamos fazer a associação desses resistores.

R 24 // R 40 = 24 ⋅ 40 24 + 40

R 24 // R 40 = 960 64

R 24 // R 40 = 15 K Ω

O resistor de 10 K Ω está em paralelo com o de 15 Ω .

R 10 // R 15 = 10 ⋅ 15 10 + 15

R 10 // R 15 = 150 25

R 10 // R 15 = 6 K Ω

Passo 4

Estamos quase terminando. Saca só como o circuito tá agora.

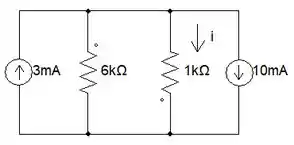
Mais uma vez, temos duas fontes de corrente em paralelo, vamos soma-las e acharmos o equivalente.

i e q 2 = i 3 + i e q

i e q 2 = 3 m - 10 m

i e q 2 = - 7 m A

Boaaaa. Agora que temos uma fonte de corrente equivalente, iremos fazer divisor de corrente nos e acharmos o i . Vamos lá!

i = i e q 2 ⋅ R 6 R 1 + R 6

i = - 7 m ⋅ 6 K 1 K + 6 K

i = - 6 m A

Iae, foi de boa? Bora continuar!

Resposta

i = - 6 m A

Exercícios de Livros Relacionados

25- Determine v o no circuito da Figura 4.93 usando transformações de fontes. Verifique seu resultado usando o P S p i c e ou M u l t i S i m
20- Use transformação de fontes para reduzir o circuito da Figura 4.88 a uma única fonte de tensão em série com um único resistor.
22- Para o circuito da Figura 4.90 , use transformação de fontes para determinar i .
21- Usando a Figura 4.89 , elabore um problema para ajudar outros estudantes a entender melhor a transformações de fontes.
30- Use transformação de fontes no circuito mostrado na Figura 4.98 para determinar i x .