Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 9.7 - Ex. 3

Para t > 0 no EX. 9.7 . 2 , calcule:

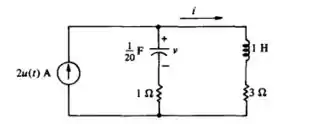
a) v

b) i

Passo 1

Fala aí pessoal tudo blz?

Nessa questão para t > 0 no EX. 9.7 . 2 , calcule:

a) v

b) i

Confia e vem comigo.

Passo 2

Sabendo que na letra (a) para,

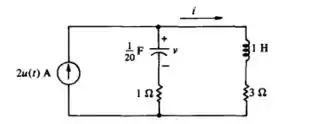
Temos,

R i + (d i)/(d t) = v

Ficando,

x_n = A_1 e^((alpha + beta) t) + A_2 e^((alpha - beta) t) ,

Chegando em,

x_n = e^(- 2 t) (- 6 cos 4 t + 7 sin 4 t) + 6 V

Na letra (b) para achar i temos,

R i + (d i)/(d t) = v

Derivando a função,

x_n = (alpha + beta) A e^((alpha + beta) t) - (alpha + beta) A e^((alpha - beta) t)

Chegando em,

x_n = e^(- 2 t) ( - 2 cos 4 t - (1)/(2) sin 4 t + 2 A

Espero ter ajudado, bons estudos e até a próxima.

Resposta

a) x_n = e^(- 2 t) (- 6 cos 4 t + 7 sin 4 t) + 6 V

b) x_n = e^(- 2 t) ( - 2 cos 4 t - (1)/(2) sin 4 t + 2 A

Exercícios de Livros Relacionados

Calcule i para t0 se i_1 (0) = 0 A e i (0) = 3 A
Calcule v no problema 9.4, se i ( 0 ) for mudado para 2 A
Calcule v para t0 , se o circuito está em regime permanente em t = 0
Calcule i para t0 se i (0) = 4 A e v (0) = 8 V
Calcule i para t0 , se o circuito está em regime permanente em t = 0 -