Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 6.Problemas - Ex. 42

Se a forma de onda da tensão na figura 6.67 for aplicada aos terminais de um indutor de 5 H , calcule a corrente através do indutor. Suponha i 0 = - 1 A .

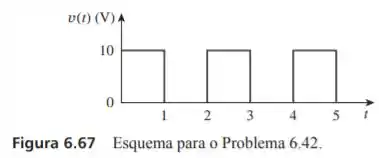
Passo 1

Nos foi fornecida a forma de onda da tensão em função do tempo para o nosso indutor. Sendo assim, podemos perceber que a nossa corrente vai ser dada por intervalos e devemos nos lembrar ainda que a tensão em um indutor é dada por

V = L ⋅ d i d t         i

Onde L é a constante de proporcionalidade que chamamos de indutância do indutor. Portanto, para encontrarmos a expressão da corrente em função do tempo devemos integrar a nossa expressão de v t para cada intervalo de tempo e suas respectivas condições iniciais. Assim, façamos as seguintes manipulações com a equação i

V = L ⋅ d i d t → V   d t = L   d i → V L   d t = d i  

Integrando ambos os lados de 0   a   t e substituindo a expressão dada no enunciado para v t vamos obter

i t =   1 L ⋅ ∫ 0 t v t   d t + i 0

Passo 2

Então, teremos para o intervalo de 0 < t < 1

i t = 10 5 ⋅ ∫ 0 t   d t - 1 = 2 t - 1   A

Procedendo da mesma forma para todos os outros intervalos vamos obter

Para 1 < t < 2

i t = 0 + i 1 = 1 A

Para 2 < t < 3

i t = 10 5 ⋅ ∫ 2 t   d t + i 2 = 2 t - 3   A

Para 3 < t < 4

i t = 0 + i 3 = 3 A

Para 4 < t < 5

i t =   10 5 ⋅ ∫ 5 t   d t + i 4 = 2 t - 5 A

Pronto, está resolvido nosso problema.

Resposta

i t = 2 t - 1 A ,       0 < t < 1 1 A ,     1 < t < 2   2 t - 3 A ,       2 < t < 3 3 A ,       3 < t < 4   2 t - 5 ,       4 < t < 5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Elabore um problema para ajudar outros estudantes a entenderem melhor como os indutores funcionam.
A corrente através de um indutor de 40 m H é dada por i t = 0 ,t0 t ⋅ e - 2 tA ,t0 Determine a tensão v t .
Um indutor possui uma mudança linear na corrente variando de 50 m A a 100 m A em 2 m s e induz uma tensão de 160 m V . Calcule o valor do indutor.
A corrente em um indutor de 80 m H aumenta de 0a60 m A . Qual é a quantidade de energia armazenada no indutor?
Para o circuito da figura 6.70, calcule o valor de R que fará a energia armazenada no capacitor ser a mesma que aquela armazenada no indutor em CC.