Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 7.2 - Ex. 3

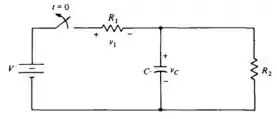
Na Fig. 7.4, considere que C = 1/4 F, R1 = R2 = 4 Ω e V = 20 V. Se a corrente em R2 em t = 0- é 2A no sentido para baixo, calcule em t = 0- e em t = 0+ (a) a carga no capacitor, (b) a corrente em R1 que flui para a direita, (c) a corrente no capacitor C que flui para baixo e (d) dvc/dt.

Passo 1

Falaa galerinhaa!!! Tudo tranquilo?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede analisarmos o circuito em relação à um capacitor. Parece muita coisa, mas vai ser tranquilo. Partiu??

Passo 2

Bom, para o item a) como queremos descobrir a carga no capacitor devemos lembrar da relação com a tensão. Responde Aí!! Lembrou?? Não?!

q = C   ∙ v

Assim em t = 0 - , vamos ter a chave fechada, resultando no circuito completo.

Pela Lei de Ohm, em R2 a tensão será:

V 2 = R 2   ∙ i 2 = 4   ∙ 2 = 8   V

Como o capacitor e R2 estão em paralelo, as tensões são as mesmas, portanto pela equação de carga:

q = C   ∙ v = 0,25   ∙ 8 = 2 C

Agora vamos considerar em t = 0 + :

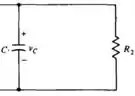
Nesse momento a chave está aberta, resultando em apenas parte do circuito.

Como v c   0 - = v c 0 + = 8 V

Assim: q = C   ∙ v = 0,25   ∙ 8 = 2 C

No item b) queremos a corrente em R1, portanto:

Em t = 0 - , vamos ter a chave fechada, resultando no circuito completo

Como sabemos que i 2 = 2 A (corrente que passa por R2) e que v c   0 - = 8 V , podemos aplicar LKT, portanto:

- 20 + 4 i 1 + 8 = 0

Assim i 1 = 3   A

Agora vamos considerar em t = 0 + :

Nesse momento a chave está aberta, resultando em apenas parte do circuito

Como a chave está aberta, não passará corrente em R1, resultando i 1 = 0   A  

Passo 3

Já cansou?? Calma que já está acabando.

Para o item c) temos que encontrar a corrente que passa no capacitor.

Em t = 0 - , vamos ter a chave fechada, resultando no circuito completo.

Assim pela LKC, podemos dizer que:

i 1 - i 2 - i c = 0

Como já sabemos i 1   e i 2 , agora ficou fácil.

Portanto i c = 1 A

Agora vamos considerar em t = 0 + :

Nesse momento a chave está aberta, resultando em apenas parte do circuito

Como v c   0 + = 8 V , assim pela Lei de Ohm:

i c =   - 8 4 =   - 2 A

Lembrando do sinal negativo por conta de estar descarregando.

Ufaa!! Para finalizar o item d) temos que lembrar da relação da tensão com a corrente no capacitor. Essa relação é a seguinte:

i = C   ∙   d v d t

Em t = 0 - , vamos ter a chave fechada, resultando no circuito completo

Como já temos todos os dados, agora é só substituir.

  d v d t =   i C =   1 0,25 = 4   V / s

Agora vamos considerando em t = 0 + :

d v d t =   i C =   - 2 0,25 = - 8   V / s

Resposta

a)

Em t = 0 - , q = 2 C

Em t = 0 + , q = 2 C

b)

Em t = 0 - , i 1 = 3 A

Em t = 0 + , i 1 = 0 A

c)

Em t = 0 - , i c = 1 A

Em t = 0 + , i c = - 2 A

d)

Em t = 0 - , d v d t = 4   V / s

Em t = 0 + , d v d t = - 8   V / s

Exercícios de Livros Relacionados

Determine a tensão v para t0 atraves de uma associação série de um resistor de 10 Ω e um capacitor de 20 m F , se a tensao no capacitor em t = 0 é - 25V e corrente é i = 5 e - 10 tA .
i ( 0^- ) = 2 A . Calcule w_c ( 0^- ) , w_c ( 0^+ ) .
Se v ( 0^- ) = 72 V , calcule i_1 , i_2 , i_c , v_c e v em t = 0^- e em t = 0^+ .
Calcule a capacidade equivalente vista pelos terminais a-b se todas as capacitâncias são em uF.
As capacitâncias mostradas são todas em uF. Calcule a capacidade equivalente vista pelos terminais a-b.