Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 38

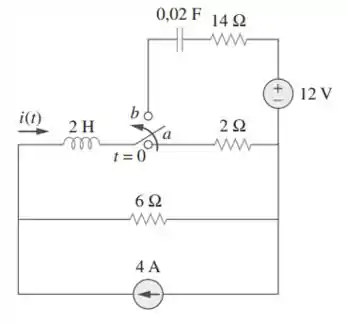
A chave no circuito da figura é movida da posição a para b (a conexão em b ocorre antes da desconexão em a) em t = 0 . Determine i ( t ) para t > 0 .

Passo 1

Vamos começar passando os elementos para o domínio de Laplace e desenhando o circuito para t < 0 (regime permanente) para facilitar a visualização:

Note que em regime permanente o indutor é um curto circuito e o capacitor é um circuito aberto.

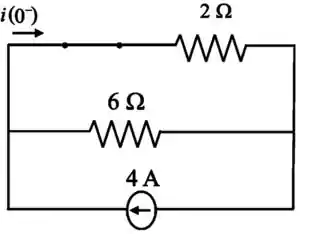
Passo 2

Vamos calcular a corrente i ( 0 - ) usando o princípio da divisão de corrente:

i ( 0 - ) = 3 A

E como o indutor não permite mudanças repentinas na corrente, então:

i ( 0 ) = i ( 0 + ) = i ( 0 - ) = 3 A

Passo 3

Agora, vamos fazer o circuito para t > 0 e já desenhá-lo no domínio de Laplace:

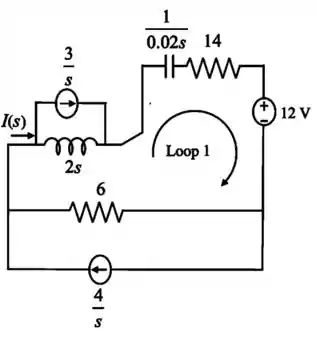
Passo 4

Aplicando agora a lei das tensões de Kirchhoff na malha 1 (Loop 1), obtemos I ( s ) :

2 s [ I ( s ) - 3 s ] + I ( s ) [ 1 0.02 s ] + 14 I ( s ) + 12 s + 6 [ I ( s ) - 4 s ] = 0

I ( s ) = 3 s + 6 ( s + 5 ) 2

Passo 5

Separando em frações parciais teremos:

I ( s ) = 3 s + 6 ( s + 5 ) 2 = A ( s + 5 ) + B ( s + 5 ) 2

Agora basta encontrar A   e   B   :

A = 3

B =   - 9

Daí, substituindo, teremos:

I ( s ) = 3 s + 6 ( s + 5 ) 2 = 3 ( s + 5 ) - 9 ( s + 5 ) 2

Por Laplace utilizando a tabela de transformadas, teremos:

i ( t ) = [ 3 e - 5 t - 9 t   ×   e - 5 t ]   u ( t )     A , t>0.

Resposta

i ( t ) = [ 3 e - 5 t - 9 t   ×   e - 5 t ]   u ( t )     A , t>0.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine v para t0 no circuito da figura:
Para o circuito na figura, determine i ( t ) para t0 .
Determine v ( t ) para t0 no circuito da figura.
Consulte o circuito da figura. Calcule i ( t ) para t0 .