Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 39

Para o circuito na figura, determine i ( t ) para t > 0 .

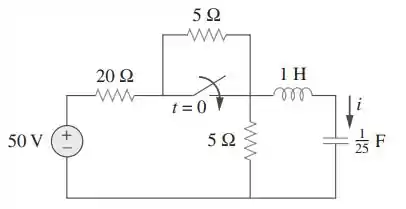
Passo 1

Vamos começar passando os elementos para o domínio de Laplace e desenhando o circuito para t < 0 (regime permanente) para facilitar a visualização:

Note que em regime permanente o indutor é um curto circuito e o capacitor é um circuito aberto.

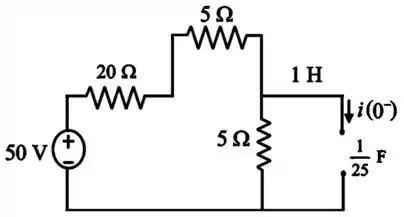
Passo 2

Claramente, pela figura, a corrente i ( 0^- ) = 0 A

E como o indutor não permite mudanças repentinas na corrente, então:

i ( 0^- ) = i ( 0^+ ) = i ( 0^() ) = 0 A

Com isso, vamos representar o circuito para t > 0 já em Laplace:

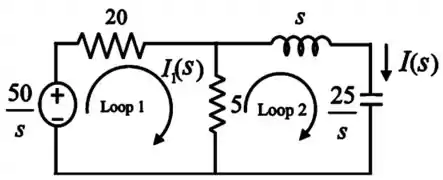
Passo 3

Agora, vamos aplicar a Lei das tensões de Kirchhoff na malha 1 (Loop 1):

- (50)/(s) + 20 I_1 ( s ) + 5 [ I_1 ( s ) - I ( s ) ] = 0

I_1 ( s ) = (1)/(25) [ (50)/(s) + 5 I ( s ) ]

Passo 4

Em seguida, aplicamos a lei das tensões de Kirchhoff na malha 2 (Loop 2)

s I ( s ) + (25)/(s) I ( s ) + 5 [ I ( s ) - I_1 ( s ) ] = 0

I ( s ) = 5 I_1 ( s ) [ (s)/(s^2 + 5 s + 25) ]

Passo 5

Agora, é só substituir I_1 ( s ) em I ( s ) :

I ( s ) = (10)/(s^2 + 4 s + 25) = (10)/([ s - ( - 2 + j 4.5825 ) ] [ s - ( - 2 - j 4.5825 ) ])

Passo 6

Separando em frações parciais teremos:

I ( s ) = (10)/(s^2 + 4 s + 25) = (10)/([ s - ( - 2 + j 4.5825 ) ] [ s - ( - 2 - j 4.5825 ) ]) = (A)/([ s - ( - 2 + j 4.5825 ) ]) + (B)/([ s - ( - 2 - j 4.5825 ) ])

Agora basta encontrar A e B :

A = - j 1.091

B = j 1.091

Daí, substituindo, teremos:

I ( s ) = (- j 1.091)/([ s - ( - 2 + j 4.5825 ) ]) + (i 1.091)/([ s - ( - 2 - j 4.5825 ) ])

Por Laplace utilizando a tabela de transformadas, teremos:

i ( t ) = - j 1.091 [ e^(( - 2 + j 4.5825 ) t) - e^(( - 2 - j 4.5825 ) t) ] u ( t ) A .

Resposta

i ( t ) = - j 1.091 [ e^(( - 2 + j 4.5825 ) t) - e^(( - 2 - j 4.5825 ) t) ] u ( t ) A .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o circuito da figura, calcule i ( t ) para t0 .
Considere a figura e elabore um problema para ajudar outros estudantes a entender melhor como usar o teorema de Thévenin (no domínio s) para ajudar na análise de circuito.
Para o circuito da figura, determine v ( t ) para t0.
Obtenha v ( t ) e i ( t ) para t0 , no circuito da figura:
A chave no circuito da figura movida da posição A para B em t = 0 (note que a chave deve ser conectada em B antes de interromper a conexão em A). Determine i ( t ) para t0 . Considere também que a ten