Determine para no circuito da figura.
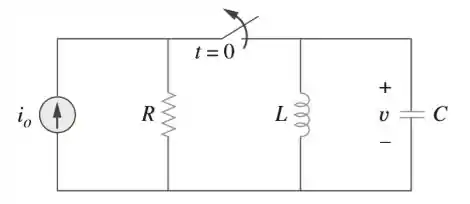
Passo 1
Em temos a chave fechada e o circuito em regime permanente. Nesse caso, o capacitor age como um circuito aberto e o indutor, como um curto circuito.
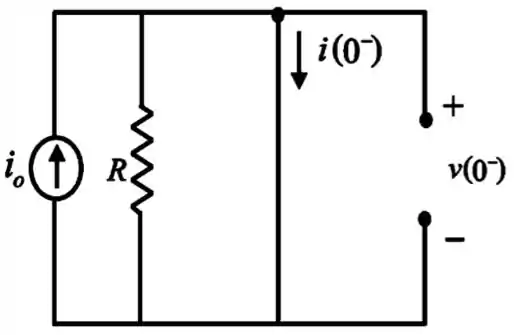
Passo 2
Observando a figura, vemos que porque temos toda a corrente da fonte passando por um curto circuito.
Como não pode haver mudança repentina na corrente de um indutor, temos:
Observando a figura, também conseguimos concluir que e como no capacitor não pode haver mudança repentina na tensão, então:
Passo 3
Em a chave abre, então, aqui, vamos representar esse momento já em domínio de Laplace (s):
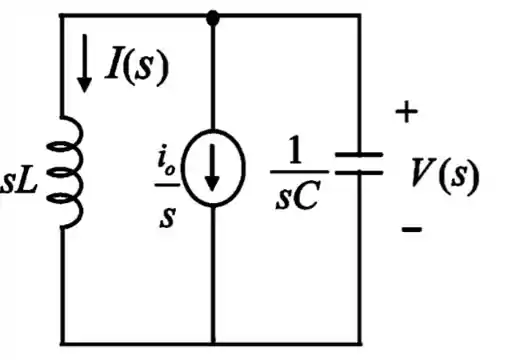
Passo 4
Aplicando a análise nodal no nó de cima e isolando , teremos:
Passo 5
Pra finalizar, vamos aplicar a inversa utilizando nossas fórmulas de Laplce:
Vamos lá: