Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 37

Determine v para t > 0 no circuito da figura:

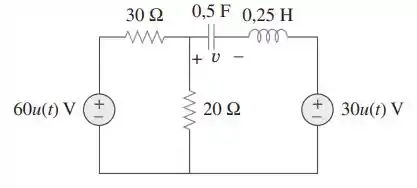
Passo 1

Vamos começar passando os elementos para o domínio de Laplace e desenhando o circuito para t > 0 para facilitar a visualização:

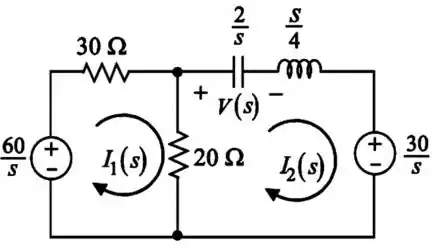
Passo 2

Agora, vamos aplicar a lei das tensões de Kirchhoff na malha 1:

- (60)/(s) + 30 I_1 ( s ) + 20 [ I_1 ( s ) - I_2 ( s ) ] = 0

I_1 ( s ) = (20 I_2 ( s ) + (60)/(s))/(50)

E depois, a lei das tensões de Kirchhoff na malha 2:

20 [ I_2 ( s ) - I_1 ( s ) ] + (2)/(s) I_2 ( s ) + (s)/(4) I_2 ( s ) + (30)/(s) = 0

Com essas equações podemos isolar nosso I_2 ( s ) :

I_2 ( s ) = (- 120)/(5 s^2 + 240 s + 40)

Passo 3

Agora, queremos uma expressão para a tensão que passa no capacitor v ( t ) para t > 0

Observando a figura 1 temos:

V ( s ) = (2)/(s) I_2 ( s )

Substituindo o nosso I_2 ( s ) na expressão, temos:

V ( s ) = (- 48)/(s ( s + 0.1672 ) ( s + 47.84 ))

Passo 4

Separando em frações parciais teremos:

V ( s ) = (- 48)/(s ( s + 0.1672 ) ( s + 47.84 )) = (A)/(s) + (B)/(( s + 0.1672 )) + (C)/(( s + 47.84 ))

Agora basta encontrar A , B e C :

A = - 6

B = 6.022

C = - 0.021

Daí, substituindo, teremos:

V ( s ) = (- 6)/(s) + (6.022)/(( s + 0.1672 )) - (0.021)/(( s + 47.84 ))

Então agora, basta utilizar a tabela de transformadas de Laplace e teremos:

v ( t ) = [ - 6 + 6.022 e^(- 1672 t) - 0.021 e^(- 47.84 t) ] u ( t ) , para t>0.

Resposta

v ( t ) = [ - 6 + 6.022 e^(- 1672 t) - 0.021 e^(- 47.84 t) ] u ( t ) , para t>0.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine i ( t ) para t0 para o circuito na figura. Suponha i s t = 4 u t + 2 δ tm A .
Determine v o ( t ) no circuito da figura.
Determine v ( t ) para t0 no circuito da figura.
Calcule as correntes de malha no circuito da figura. Apresente seus resultados no domínio s.
Determine i ( t ) para t0 no circuito da figura.