Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 7.Problemas - Ex. 59
Determine a resposta ao degrau para = no circuito da Figura 7.124.
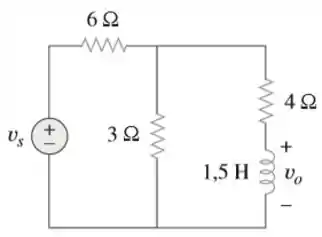
Passo 1
Seja a corrente pelo indutor.
Para
Para ,
Em , o indutor se torna curto e a corrente fornecida pela fonte de volts é
A tensão no resistor de é igual a . Portanto, a corrente através do indutor é igual a
Passo 2
Logo,
Resposta
Exercícios de Livros Relacionados
Suponha que a chave no circuito da Figura P7.51 esteve na posição a por um longo tempo e que em t = 0 ela é colocada na posição b. Determine (a) vC(0+); (b) vC(q); (c) t para t . 0; (d) i(0+); (e) vC,
A chave no circuito da Figura P7.14 esteve fechada por um longo tempo antes de abrir em t = 0. Determine vo (t) para t $ 0+.
A chave no circuito da Figura P7.15 esteve fechada por um longo tempo antes de abrir em t = 0. Determine a) i L(t), t $ 0. b) vL(t), t $ 0+. c) i Δ(t), t $ 0+.
As duas chaves mostradas no circuito da Figura P7.17 funcionam simultaneamente. Antes de t = 0, cada chave estava na posição indicada por um longo tempo. Em t = 0, elas passam instantaneamente para su
No circuito mostrado na Figura P7.19, a chave esteve na posição a por um longo tempo. Em t = 0, ela passa instantaneamente de a para b. a) Determine i o (t) para t $ 0. b) Qual é a energia total forne