Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 7.Problemas - Ex. 22

A chave do circuito mostrado na Figura P7.22 esteve aberta por um longo tempo antes de seu fechamento em t = 0. Escreva a expressão para a tensão do capacitor, v(t), para t $ 0.

Passo 1

Para t < 0 :

V 0 = ( 20000 | | 60000 ) 20 × 10 - 3

V 0 = 300   V

Passo 2

Para t ≥ 0 :

A chave está fechada neste momento, então a corrente vai ter uma preferência para passar por lá, já que não tem resistência (a corrente não gosta de dificuldades hehe), então o circuito vai ficar basicamente dessa forma:

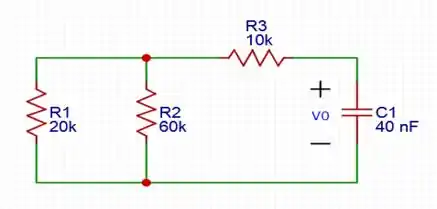
Logo, para calcular a resistência equivalente, temos a seguinte conta:

R e q = 10000 + ( 20000 | | 60000 )

R e q = 25   k Ω

Já temos a resistência equivalente e a “capacitância equivalente” (que é somente um capacitor), então já pode fazer o cálculo da constante de tempo.

τ = R e q C

τ = 25000 40 × 10 - 9 = 1   m s

1 τ = 1000

Agora, já temos todas as ferramentas necessárias para encontrar a equação da tensão do capacitor.

v t = V 0 e - t τ   ,     t ≥ 0

v t = 300 e - 1000 t ,     t ≥ 0

Resposta

v t = 300 e - 1000 t ,     t ≥ 0

Exercícios de Livros Relacionados

8.39) Calcule v para t0, se vg = 3u(t) V.
A chave do circuito mostrado na Figura P7.61 esteve na posição OFF por um longo tempo. Em t=0, ela passa instantaneamente para a posição ON. Determine v 0 tp a r at ≥ 0 .
O capacitor do circuito visto na Figura P7.76 foi carregado até 300 V. Em t=0, a chave 1 fecha-se, fazendo com que o capacitor se descarregue na rede resistiva. A chave 2 fecha-se 200 μ s depois do fe
A chave no circuito da Figura P7.64 esteve na posição x por um longo tempo. A carga inicial no capacitor de 60 nF é igual a zero. Em t=0, a chave passa instantaneamente para a posição y.Determine v 0