Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 7.Problemas - Ex. 64

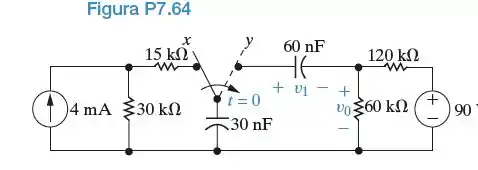
A chave no circuito da Figura P7.64 esteve na posição x por um longo tempo. A carga inicial no capacitor de 60 nF é igual a zero. Em t=0, a chave passa instantaneamente para a posição y.

  1. Determine v 0 t   p a r a   t ≥ 0 + .
  2. Determine v 1 t   p a r a   t ≥ 0 .

Passo 1

Falaaa, pessoal! Como vocês estão?

Bora pra mais uma questãozinha pra exercitar o que a gente sabe sobre resposta de circuitos RL e RC de primeira ordem!

  1. Nesse item, podemos começar ilustrando nossa situação:

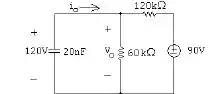
    2. Com isso, podemos escrever que:

    v ∞ = 60 180 90 = 30   V

    E mais, temos:

    R e q = 60 | | 120 = 40 k Ω

    T = R e q C = 0,8   m s

    Por fim, temos que:

    v 0 = 30 + 90 e - 1250 t V

    Passo 2

  2. Começamos com as seguintes relações:

i 0 = v 0 60000   90120000 = 2,25 e 1250 t m A

Ou seja:

v 1 = - 30 e - 1250 t + 30 V

Resposta

  1. v 0 = 30 + 90 e - 1250 t V

v 1 = - 30 e - 1250 t + 30 V

Exercícios de Livros Relacionados

Mostre que x 1 = A 1 e - 2 t e x 2 = A 2 e - 3 t são soluções de d 2 x d t 2 + 5 d x d t + 6 x = 0 Independentemente do valor das constantes A 1 e A 2 .
Mostre que se o membro da direita da equação diferencial do Ex. 9.2.1 é alterado de 0 para 12 , então x = A 1 e - 2 t + A 2 e - 3 t + 2 É uma solução. Então a resposta natural é A 1 e - 2 t + A 2 e -
Dado(a) d 2 x d t 2 + 7 d x d t + 10 x = 0 (b) d 2 x d t 2 + 4 d x d t + 4 x = 0 Calcule a equação característica e as frequências naturais em cada caso.
Dada a equação diferencial não-linear x d 2 x d t 2 - t d x d t = 0 Mostre que x 1 = t 2 e x 2 = 1 são soluções mas x 1 + x 2 não é uma solução.
Dada a equação diferencial linear t - 1 d 2 x d t 2 + t - 2 d x d t = 0 Mostre que x 1 = t e - t , x 2 = 1 e x 1 + x 2 são soluções.