Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 7.Problemas - Ex. 23
A chave no circuito da Figura P7.23 esteve na posição esquerda por um longo tempo. Em t = 0, ela passa para a posição direita, onde permanece. a) Escreva a expressão para a tensão do capacitor, v(t), para t $ 0. b) Escreva a expressão para a corrente que passa pelo resistor de 40 kV, i(t), para t $ 0+.
Passo 1
Para :
Necessitamos saber do comportamento em t
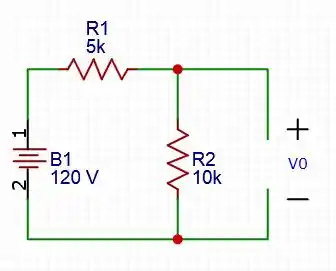
Para calcular , basta fazer um divisor de tensão:
Para : a chave muda de posição, logo o circuito também se modifica, desse jeito aqui:
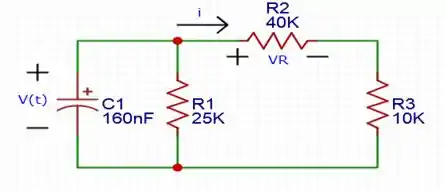
Para a resistência equivalente, temos a seguinte conta:
Se temos a resistência equivalente, temos também a constante de tempo:
Com isso, podemos fazer a equação da tensão do capacitor
Passo 2
[b] – Já sabemos que a tensão no capacitor é igual a , então, para encontrar a tensão no resistor de é necessário um divisor de tensão
No caso da corrente , é só dividir o pela resistência