Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas - Ex. 54

Considere a Figura 8.100 e elabore um problema para ajudar outros estudantes a entenderem melhor os circuitos de segunda ordem gerais.

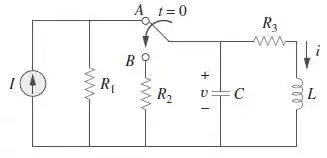
Passo 1

Já que o problema pede para criarmos um exercício, vamos fazer esse aqui:

“Para o circuito dado, seja I = 9   A ,   R 1 = 40   Ω ,   R 2 = 20   Ω ,   C = 10   m F ,   R 3 = 50   Ω e L = 20   m H . Determine (a) i ( 0 + ) e v 0 + ; (b) d i 0 + d t e d v 0 + d t ; (c) i ( ∞ ) e v ∞ .

Vamos para a solução, então! Na letra (a), no instante t = 0 - (anterior a mudança da chave), a chave está em A e está no regime permanente. O circuito a seguir mostra essa situação:

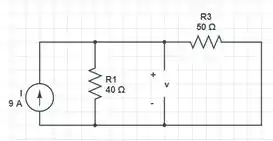
Com a chave na posição A , a corrente i ( 0 - ) que passa pelo resistor de 50   Ω pode ser encontrada através do divisor de corrente:

i 0 - = 40 50 + 40 9 = 4   A

A tensão v é a mesma que está no resistor de 50   Ω . Portanto,

v 0 - = 50 × i = 200   V

Como a corrente fluindo através do indutor não pode mudar tão rapidamente, temos que i 0 + = i 0 - = 4   A . O mesmo pensamento se aplica para a tensão no capacitor, nos levando a ter v 0 + = v 0 - = 200   V .

Passo 2

Vamos agora para a letra (b). A tensão em cima do indutor pode ser expressa pela equação v L = L d i d t , ou v L 0 + L = d i 0 + d t . No tempo t = 0 + , a malha da direita nos dá a seguinte equação:

- v 0 + + 50 × 4 + v L 0 + = 0

- 200 + 200 + v L 0 + = 0

v L 0 + = 0

L d i 0 + d t = 0

Como o valor de L é diferente de zero, temos que d i 0 + d t deve ser igual a zero!

Agora, para o capacitor, podemos escrever a corrente que flui através dele como i C = C d v d t ou d v 0 + d t = i C C . No tempo t = 0 + , a chave muda para a posição B e, analisando as correntes que entram e saem do nó de cima do capacitor, temos

200 20 + i C + 4 = 0

i C = - 14   A

Logo, podemos encontrar o valor para d v 0 + d t :

d v 0 + d t = - 14 0,01 = - 1,4   k V / s

Passo 3

Por fim, na letra (c) queremos saber como fica a corrente i e a tensão v num tempo muito longo. Bom, como para t > 0 a chave está na posição B, não temos mais uma fonte alimentando o circuito. Sendo assim, os valores de i e v irão decair para zero conforme o tempo passar. Logo,

i ∞ = v ∞ = 0

Resposta

  1. i 0 + = i 0 - = 4   A e v 0 + = v 0 - = 200   V ;
  2. d i 0 + d t = 0 e d v 0 + d t = - 1,4   k V / s ;
  3. i ∞ = v ∞ = 0 .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule x , se d 2 x d t 2 + 25 x = 0
Se a tensão nodal no nó b da Fig. 9.3 é v 1 , mostre que as duas equações nodais são v - v g 4 + v - v 1 R + 1 4 d v d t = 0 E v 1 - v g R + ∫ 0 t v 1 d t + i 0 = 0 Diferencia a segunda destas equaçõe
Calcule a resposta forçada se d 2 x d t 2 + 4 d x d t + 3 x = f t Onde f ( t ) é dada por a6 ,b 8 e - 2 t ,c 6 t + 14 .
Se x 0 = 4 e d x 0 d t = - 2 , calcule a solução completa no Ex. 9.5.1.
Calcule a resposta completa se d 2 x d t 2 + 9 x = 18 s e n 3 t E x 0 = d x 0 d t = 0 Sugestão: Verifique x f = t ( A c o s 3 t + B s e n 3 t )