Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 14.Problemas - Ex. 95
Um circuito de antena sintonizado em série é formado por um capacitor variável ( a ) e uma bobina de antena de que possui uma Resistência igual a .
- Determine o intervalo de frequência de sinais de rádio para o qual o rádio pode ser sintonizado.
- Determine o valor de em cada extremidade do intervalo de frequências.
Passo 1
Bem, o circuito da antena de rádio é pelo visto um circuito RLC em série como esse daqui:
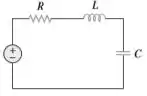
A gente costuma dizer que o rádio está sintonizado quando ele possui a mesma frequência (frequência de ressonância) que o circuito que o recebe (o circuito RLC). Ora, no nosso caso de um circuito em série, da teoria sabemos que tal frequência é dada por...
Quando você gira aquele botão grande em um aparelho de rádio de carro, por exemplo...
O que você está fazendo na prática é variando o capacitor variável e mudando a frequência de ressonância (ou a frequência da sua rádio)!
Passo 2
Beleza, com isso, então no nosso caso, quando o capacitor variável está em , a frequência do Radio será:
E quando a gente gira aquela rodinha que sintoniza o Rádio, a gente coloca o capacitor valendo , sintonizando então, a frequência de...
Logo, a faixa de frequência que pode ser sintonizado por esse rádio é de:
Passo 3
Podemos encontrar o , ou fator de qualidade, pela equação:
No primeiro extremo da frequência ():
No segundo extremo da frequência ():
Resposta
Letra A)
Letra B)