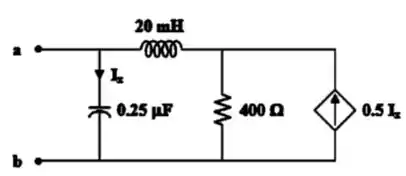
- Para o circuito da figura, desenhe o novo circuito após este ter sofrido aplicação de escala de
- Obtenha a impedância equivalente de Thévenin nos terminais a-b do circuito que sofreu a aplicação de escala em
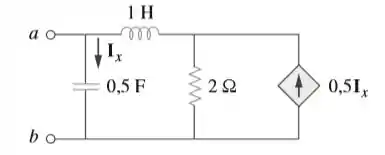
Passo 1
Nessa questão, nós queremos encontrar os valores de . Sabendo que Então, vamos utilizar a seguinte fórmula:
Para o resistor:
Para o indutor:
Para o capacitor:
Passo 2
Agora, podemos desenhar o novo circuito:

Passo 3
Agora, o que vamos fazer é inserir uma fonte de tensão de teste de entre os terminais e daí teremos esse circuito, já no domínio de Laplace:
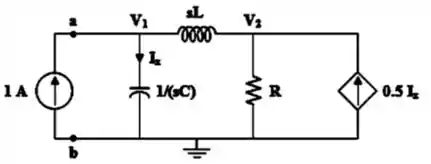
E agora, vamos uma análise nodal nos nós 1 e 2:
Nó 1:
(1)
Nó 2:
Mas como
(2)
Resolvendo o sistema de (1) com (2), chegamos no valor de :
Para encontrar a resistência de Thévenin:
Passo 4
Como ele quer o na frequência de , basta substituir tudo que for por e daí é só substituir pelo valor de que temos.
Chegaremos em:
ou, em polar: