Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 14.Problemas - Ex. 26

Elabore um problema para ajudar outros estudantes a entender melhor ω 0 , Q e B na ressonância em circuitos R L C em série.

Passo 1

Bem, existem várias formas de responder esse item corretamente, mas eu, Responde Aí, acho que a forma mais simples e interessante de se entender como encontrar esses parâmetros de um circuito RLC em série, é dando um circuito e pedindo para se calcular esses caras:

PROBLEMA: Dado o circuito RLC em série abaixo, encontre o valor de ω 0 , Q e B.

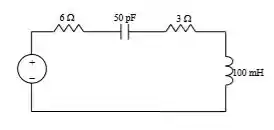
Passo 2

Poxa, de acordo com a teoria, a gente pode encontrar os valores de ω 0 , Q e B dessa forma aqui:

ω 0 = 1 L C               ,               Q = ω 0 L R                       e                   B = ω 0 Q

Então, substituindo os valores de L = 100 m H e C = 50   p F , podemos encontrar a frequência natural primeiro (lembre-se de que micro é 10 - 3 e pico é 10 - 12 )...

ω 0 = 1 100 ⋅ 10 - 3 ⋅ 50 ⋅ 10 - 12     →

ω 0 = 1 10 2 ⋅ 10 - 3 ⋅ 5 ⋅ 10 ⋅ 10 - 12     →

ω 0 = 1 5 ⋅ 10 - 12 = 1 5 ⋅ 10 - 6     →

ω 0 = 1 5 ⋅ 10 - 12 = 1 5 10 6     →

Como 1 5 ≅ 0,44721

ω 0 = 447 ⋅ 10 3 = 447,21   k r a d / s

Passo 3

Com isso podemos agora calcular o fato de qualidade Q :

Q = ω 0 L R =

447,21 ⋅ 10 3 ⋅ 100 ⋅ 10 - 3 R

Mas atenção, pois como o circuito é em série R = 3 + 6 = 9 ...

Q = 447,21 ⋅ 10 3 ⋅ 100 ⋅ 10 - 3 9 =

447,21 ⋅ 100 9 = 4,969

Passo 4

Por fim, podemos agora encontrar a Largura de banda para o circuito série:

B = ω 0 Q = 447,21 ⋅ 10 3 4,969 =

90 ⋅ 10 3   r a d   / s

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine vo(t) no circuito da Figura 16.82 se vx(0) = 2 V e i(0) = 1 A.
Determine a transformada de Laplace da tensão mostrada na figura. Usando o valor de v s ( t ) no circuito mostrado na figura, determine o valor de v o ( t ) .
Considere o circuito RLC mostrado na figura e determine a resposta completa se v ( 0 ) = 2V quando a chave é fechada.
Determine i 0 ( t ) para t0 no circuito da figura.
A função na figura é movida da posição 1 para a 2 em t = 0 . Determine v ( t ) para todo t0 .