Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 14.Problemas - Ex. 29
Seja no circuito da Figura. Determine , e , visto pelo capacitor.
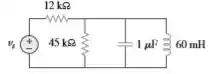
Passo 1
Primeira coisa aqui é transformar esse circuito em um paralelo já , e se resolvem pelas mesmas formulações:
Passo 2
Para transformar esse circuito em paralelo, podemos transformar essa fonte de tensão e essa impedância de em uma fonte de corrente e uma impedância de em paralelo...
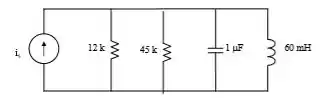
Onde a fonte de corrente é calculada pela Lei de Ohm:
Mas isso até que não é tão relevante aqui, já que precisamos mesmo calcular esses caras aqui...
Cuidado! Porque esse aí nas fórmulas se refere ao equivalente. Para encontra-lo, basta fazer o paralelo entre e ...
Passo 3
Finalmente podemos encontrar os valores procurados simplesmente por substituição dos valores:
Para ...
E para o ...
Resposta
Exercícios de Livros Relacionados
Considere o circuito RLC em paralelo da figura. Determine v ( t )ei ( t ) dado que v ( 0 ) = 5 e i ( 0 ) = 2A
Considere a Figura 16.81 e elabore um problema para ajudar outros estudantes a entender melhor a análise de circuitos no domínio s em circuitos com fontes dependentes.
Determine a resposta v R ( t ) para t0 no circuito da figura. Seja R = 3 Ω ,L = 2 HeC = 1 8 F .
Considere a figura e elabore um problema para ajudar outros estudantes a entenderem melhor o cálculo de tensões nodais no domínio s.
A função de transferência de certo circuito é H ( s ) = 5 s + 1 - 3 s + 2 + 6 s + 4 Determine a resposta ao impulso do circuito.