Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 8
8. No circuito da figura determine a potência média absorvida pelo resistor de .
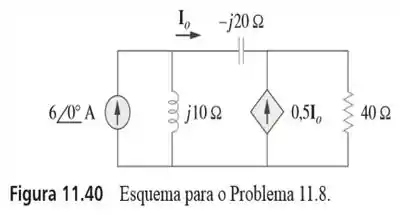
Passo 1
Como vimos na teoria, apenas cargas resistivas absorvem potência. Capacitores e indutores não absorvem potência. Vamos calcular a potência absorvida pelo resistor através da fórmula:
Passo 2
Precisamos encontrar a corrente que passa pelo resistor. Para isso, vamos fazer uma análise nodal no circuito.
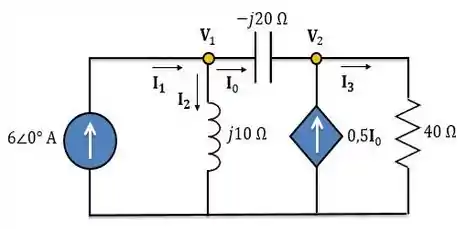
Aplicando a ao nó :
Substituindo pelas tensões nodais correspondentes:
Aplicando a ao nó :
Substituindo:
Passo 3
Isolando na primeira equação:
E agora, substituindo na seguda:
Passo 4
Pela lei de Ohm, temos no resistor de :
Passo 5
Agora que temos a corrente que passa pelo resistor de . Podemos encontrar a potência média absorvida por esse resistor através da fórmula:
Resposta
Exercícios de Livros Relacionados
35- Um ciclo de uma forma de onda periódica é representado na Figura 11.66 . Determine o valor eficaz da tensão. Note que o ciclo se inicia em t = 0 e termina em t = 6s
34- Determine o valor eficaz de f ( t ) definida na Figura 11.65
32- Obtenha o valor R M S da forma de onda corrente mostrada na Figura 11.63 .
33- Determine o valor R M S para a forma de onda na Figura 11.64
37- Elabore um problema para ajudar outros estudantes a entender melhor como determinar o valor R M S da soma de correntes múltiplas