Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 85
85- Um sistema residencial comum de um circuito trifilar monofásico permite a operação de eletrodomésticos de , bem como de , ambos a . O circuito residencial tem como modelo aquele mostrado na Figura . Calcule:
As correntes e .
A potência complexa total fornecida.
O fator de potência para todo o circuito.
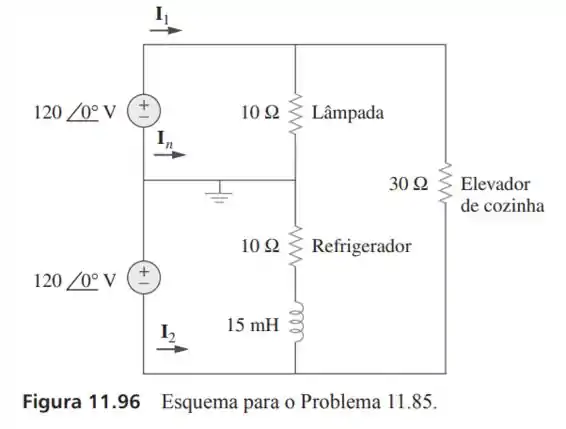
Passo 1
A reatância do indutor do refrigerador é de:
Agora vamos desenhar esse circuito com as correntes em cada malha.
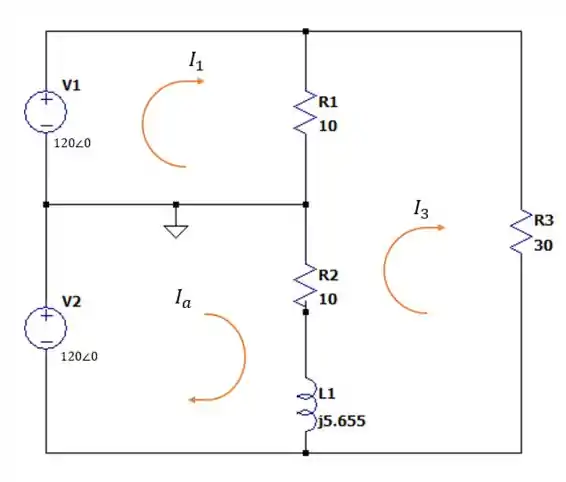
Fazendo a somatória das tensões na malha nós temos:
A somatória das tensões na malha :
E na malha :
Onde:
Passo 2
Da primeira equação podemos tirar que:
A segunda equação nos mostra que:
Substituindo tudo na equação que encontramos na terceira malha nós teremos:
Dessa forma:
Só que o sentido que desenhamos está o contrário do retrado no desenho então:
E será:
Passo 3
A potência complexa total será a potência fornecida pelas duas fontes.
Considerando que as duas fontes estão em temos:
Pois é a corrente que sai do terminal positivo.
Passo 4
O fator de potência será:
Onde no passo anterior temos:
Logo:
Fator atrasado, pois a potência reativa é positiva se configurando numa carga indutora (o indutor do refrigerador no caso.