Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 59
No circuito da Figura 13.124, faça . Determine a potência média liberada para cada resistor.
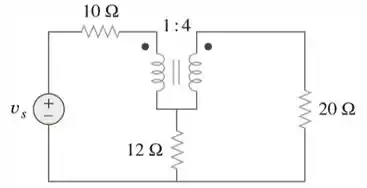
Passo 1
BOOYAAAH! Eae galera, tudo bein com vocês? Hoje vamos mecher com transformadores, e vai ser muito daora porque é um assunto incrível e ao mesmo tempo desafiador. Portanto, vamos mastigar essa questão passo a passo pra dar tudo bom! Sem mais delongas, vamos pra tão esperada questão!
Passo 2
Para o circuito abaixo, fazemos uma analise de malhas!
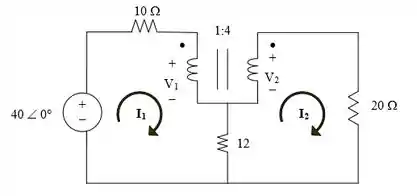
Para a malha 1,
Para a malha 2,
Nos terminais do transformador,
Passo 3
Colocando isso tudo em forma de matrizes, teremos:
Resolvendo isso, temos as potencias:
Para resistor de 10 Ohms
Para o resistor de 12 Ohms
Para o resistor de 20 Ohms
Resposta
Exercícios de Livros Relacionados
43. Obtenha V 1 e V 2 no circuito do transformador ideal da Figura 13.108.
Um transformador ideal de 440 / 110V pode ser conectado para se tornar um autotransformador ideal de 550 / 440V . Existem quatro ligações possíveis, duas das quais estão erradas. Determine a tensão de
Na Fig. 16.2(a), N 2 = 500 espiras e ϕ 21 = 200 μ W b , quando i 1 = 2A . Determine v 2 se i 1 = 10 c o s 100 tA .
Calcule a frequência para a qual a impedância refletida na figura 16.14 é real, se L 2 = 2HeZ 2 é um resistor 6Ω em série com um capacitor de 1 32 F
Dado: V g = 100 / 0 ° V , Z g = 40Ω ,L 1 = 0,5H ,L 2 = 0,1H ,M = 0,1Hew = 100 r a d s . Se Z 2 = 10 - j 1000 w Ω . Calcule:Se o ponto de polaridade estiver no terminal inferior do secundárioa) Z i n ;