Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 70
No circuito do transformador ideal da Figura , determine a potência média liberada para a carga.
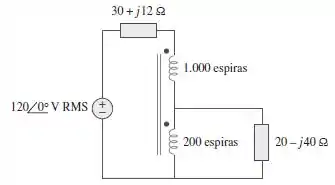
Passo 1
Pessoal, vamos aplicar a lei das malhas na malha da esquerda:
Similarmente, aplicando a lei das malhas na malha da direita:
Passo 2
A relação entre as tensões, correntes e enrolamentos é dada por:
Assim,
Substituindo as equações e na equação , temos:
E ainda substituindo a equação na equação encontrada acima:
A corrente no secundário do autotransformador é igual a:
Passo 3
A potência complexa fornecida à carga é dada por:
Sabemos que a corrente rms pode ser escrita como:
Assim,
Assim, a potência média entregue à carga é:
Resposta
A potência média entregue à carga é:
Exercícios de Livros Relacionados
O sistema trifásico de uma torre distribui energia elétrica com uma tensão de linha de 13.2 k V . Um transformador em um poste conectado a um único fio e a terra abaixa a alta tensão para 120 V r m s
Um transformador de 4 k V A , 2.400 / 240 V tem 250e s p i r a s no primário. Calcule:a) A relação de espirasb) O número de espiras no secundárioc) As correntes no primário e no secundário
Um transformador de distribuição de 25.000 / 240V r m s tem uma corrente primária de valor nominal 75 A .a)Determine o valor nominal em k V A para esse transformadorb)Calcule a corrente no secundário.
Um transformador de potência de 240 / 120 V r m s tem valor nominal 10k V A . Determine a relação de espiras, a corrente no primário e a corrente no secundário.
Um transformador com 2400e s p i r a s no primário e 48e s p i r a s no secundário é usado como casador de impedâncias. Qual é o valor refletido de uma carga de 3Ω conectada ao secundário?