Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 24

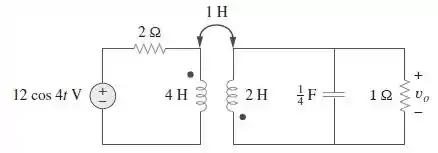
No circuito da figura 13.93 ,

  1. Determine o coeficiente de acoplamento
  2. Calcule v 0
  3. Determine a energia armazenada nos indutores acoplados em t = 2   s .

Passo 1

Galera, na letra (a) queremos achar o coeficiente de acoplamento. Ele pode ser encontrado através da seguitne equação:

k = M L 1 L 2

Substituindo os valores, temos:

k = 1 4 × 2 = 0,354

Passo 2

Vamos transformar os elementos do circuito do domínio do tempo para o domínio da frequência:

4 cos ⁡ 4 t   V   →     4 ∠ 0 °   ,   ω = 4   r a d / s

4   H   →     j ω L = j 4 4 = j 16   Ω

1 H   →     j ω L = j 4 1 = j 4   Ω

2 H   →     j ω L = j 4 2 = j 8   Ω

1 4 F   →   1 j ω C = 1 j 4 1 4 = - j   Ω

Aplicando a lei das malhas na malha 1 , a malha da esquerda, temos:

12 = 2 I 1 + j 16 I 1 + j 4 I 2

2 + j 6 I 1 + j 4 I 2 = 12 … ( 1 )

Aplicando a lei das malhas na malha 2 , a da direita, temos:

0 = j 8 I 2 + j 4 I 1 + ( - j | 1 I 2

- j 4 I 1 = 0,5 + j 7,5 I 2

I 1 = - 1,875 + j 0,125 I 2 … ( 2 )

Substituindo a equação ( 2 ) na equação ( 1 ) , temos:

2 + j 16 - 1875 + j 0,125 I 2 + j 4 I 2 = 12

I 2 = 0,45 ∠ 102,59 °   A

Substituindo esse resultado na equação ( 2 ) :

I 1 = 0,85 ∠ - 81,22 °   A

Passo 3

Logo, para a letra (b), queremos achar o valor de v 0 . Portanto,

v 0 = I 2 × ( - j | | 1 )

v 0 = 0,45 ∠ 102,59 ° × 0,5 - j 0,5

v 0 = 0,32 ∠ 57,6 °   V

No domínio do tempo,

v 0 t = 0,32 cos ⁡ 4 t + 57,6 °   V

Passo 4

Para obtermos a energia armazenada nas bobinas acopladas, nós precisamos, primeiramente, das correntes I 1 e I 2 no domínio do tempo:

i 1 t = 0,85 cos ⁡ 4 t - 81,22 °   A

i 2 t = 0,45 cos ⁡ 4 t + 102,59 °   A

Quando t = 2   s ,

i 1 = 0,85 cos ⁡ 4 2 180 π - 81,22 ° = 0,81   A

i 2 = 0,45 cos ⁡ 4 2 180 π + 102,59 ° = - 0,42   A

O total de energia armazenada é igual a:

w = 1 2 L 1 i 1 2 + 1 2 L 2 i 2 2 + M i 1 i 2

w = 1 2 4 0,81 2 + 1 2 2 - 0,42 2 + 1 0,81 - 0,42

w = 1,15   J

Resposta

  1. k = 0,354
  2. v 0 = 0,32 cos ⁡ ( 4 t + 57,59 ° )   V
  3. w = 1,15   J
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Refaça o problema 13.22 usando o PSpice ou MultiSim.
Use o PSpice ou MultiSim para determinar as corretes de malha no ircuito da Figura 13.140 . Adote ω = 1r a d / s . Na resolução esse problema use k = 0,5 .
Use o PSpice ou MultiSim para encontrar I 1 , I 2 e I 3 no circuito da Figura 13.141 .
Use o PSpice ou MultiSim para determinar I 1 , I 2 e I 3 no circuito da Figura 13.142 .
Determine I X e V X no circuito da Figura 13.144 usando o PSpice ou MultiSim