Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 22

Determine a corrente I_0 no circuito da Figura 13.91 .

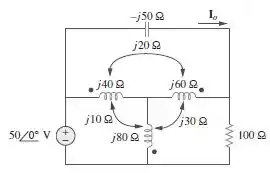
Passo 1

Bom, galerinha, considerem o circuito abaixo. Aplicando a lei das malhas para a malha 1 , temos:

50 = [j 40 (I_1 - I_3) - j 10 (I_1 - I_2) - j 20 (I_2 - I_3)] + [j 80 (I_1 - I_2) - j 10 (I_1 - I_3) + j 30 (I_2 - I_3)]

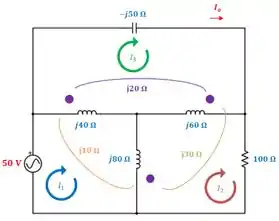
Simplificando essa equação imensa:

j 100 I_1 - j 60 I_2 - j 40 I_3 = 50 ... ( 1 )

Da mesma forma, para a malha 2 ,

0 = [j 80 (I_2 - I_1) + j 10 (I_1 - I_3) - j 30 (I_2 - I_3)] + [j 60 (I_2 - I_3) - j 20 (I_1 - I_3) - j 30 (I_2 - I_1)] + 100 I_2

Simplificando a equação:

- j 60 I_1 + (100 + j 80) I_2 - j 20 I_3 = 0 ... ( 2 )

Por fim, na malha 3 ,

0 = [j 40 (I_3 - I_1) - j 20 (I_3 - I_2) + j 10 (I_1 - I_2)] + [j 60 (I_3 - I_2) + j 30 (I_2 - I_1) - j 20 (I_3 - I_1)] - j 50 I_3

- j 40 I_1 - j 20 I_2 + j 10 I_3 = 0 ... ( 3 )

Passo 2

Temos aqui um sistema com três equações e três incógnitas. Vamos escrever esse sistema de equações em forma matricial:

[[[j,100,-,j,60,-,j,40],[-,j,60,100,+,j,80,-,j,20],[-,j,40,-,j,20,j,10]]] * [[[I_1],[I_2],[I_3]]] = [[[50],[0],[0]]]

Para resolver esse sistema podemos usar a Regra de Cramer! Vamos inicialmente achar o valor do determinante dessa matriz:

det (A) = |[[j,100,-,j,60,-,j,40],[-,j,60,100,+,j,80,-,j,20],[-,j,40,-,j,20,j,10]]|

det (A) = 60000 + j 220000

Vamos agora encontrar os determinantes de cada uma das variáveis, substituindo o vetor b em cada uma das colunas:

det (A_I_1) = |[[50,-,j,60,-,j,40],[0,100,+,j,80,-,j,20],[0,-,j,20,j,10]]|

det (A_I_1) = - 20000 + j 50000

Para a corrente I_2 ,

det (A_I_2) = |[[j,100,50,-,j,40],[-,j,60,0,-,j,20],[-,j,40,0,j,10]]|

det (A_I_2) = - 70000

Para a corrente I_3 ,

det (A_I_3) = |[[j,100,-,j,60,50],[-,j,60,100,+,j,80,0],[-,j,40,-,j,20,0]]|

det (A_I_3) = - 220000 + j 200000

Passo 3

Uma vez que temos os determinantes, basta encontrarmos os valores e cada uma das variáveis!

I_1 = (- 20000 + j 50000)/(60000 + j 220000) = 0,188 + j 0,1423

I_2 = (- 70000)/(60000 + j 220000) = - 0,08 + j 0,29

I_3 = (- 220000 + j 200000)/(60000 + j 220000) = 0,59 + j 1,161

NA nossa questão,

I_0 = I_3 = 1,3 /_ 63,06 ° A

Resposta

A corrente é igual a:

I_0 = 1,3 /_ 63,06 ° A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Detemrine I 0 no circuito da Figura 13.95 . Inverta o ponto no enrolamento da direita e calcule I 0 novamente.
Se M = 0,2H e v s = 12 cos ⁡ 10 tV no circuito da Figura 13.92 , determine i 1 e i 2 . Calcule a energia armazenada nas bobinas acopladas em t = 15m s .
No circuito da Figura 13.97 , determine o valor de X que resultará na máxima transferência de potência para a carga de 20Ω .
No circuito da figura 13.93 ,Determine o coeficiente de acoplamentoCalcule v 0 Determine a energia armazenada nos indutores acoplados em t = 2s .
Considere o circuito da Figura 13.94 e determine Z a b e I 0 .