Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 2.Problemas - Ex. 44
44. Para o circuito da Figura , calcule a resistência equivalente nos terminais .
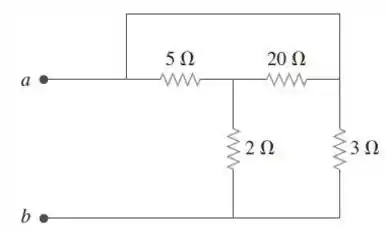
Passo 1
Bora lá resolver um probleminha sobre associação de resistores:
Vamos analisar direitinho esse circuito. Mas primeiro o que acha de indicarmos com pontos cada um dos nós importante desse circuito.
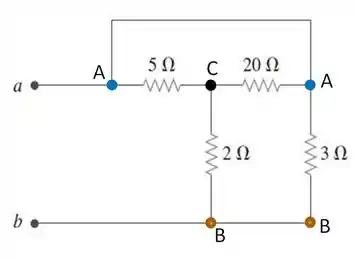
Agora, temos que analisar com calma essa imagem. O objetivo é encontrar o caminho da resistência equivalente, indo de até ou do ponto até . Vendo essa imagem acima, tiramos inicialmente que os resistores de e estão em paralelo. Calculemos a resistência equivalente para essa parte do circuito:
Esse é o caminho que vai de até . Só que existe um caminho que vai de até , né não? O que isso quer dizer?
Ora bolas, quer dizer que e a resistência na parte , que é estão em série. Assim, obtemos uma nova resistência equivalente, , que vale:
Passo 2
Por fim, temos que Essa está em paralelo com a resistência de , a qual já segue o caminho diretamente.
Desse jeito, a nossa resistência nos terminais vale...