Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 7.Problemas - Ex. 20
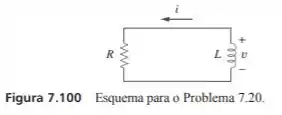
Para o circuito da figura 7.100, e ,
Determine e
Determine a constante de tempo
Calcule a energia inicial no indutor.
Que fração de energia inicial é dissipada em ?
Passo 1
Primeiramente devemos lembrar que para um circuito a constante de tempo será dada por
Lembrando que a tensão em um indutor é dada por
Substituindo em encontramos
Passo 2
Nossa constante de tempo é dada pelo inverso do expoente da exponencial que foi fornecida no enunciado, assim,
Passo 3
Por fim, a energia armazenada inicialmente no indutor será dada por
Para concluirmos o exercício resta-nos encontrar a fração da energia inicial que foi dissipada em que é encontrada fazendo
Assim, a fração que foi dissipada será
Resposta
Exercícios de Livros Relacionados
No circuito mostrado na Figura P7.19, a chave esteve na posição a por um longo tempo. Em t = 0, ela passa instantaneamente de a para b. a) Determine i o (t) para t $ 0. b) Qual é a energia total forne
A fonte de 240 V, e resistência interna de 2 V, no circuito da Figura P7.20, sofre inadvertidamente um curto-circuito em seus terminais a,b. No instante em que a falha ocorre, o circuito estava em fun
Segue o mesmo raciocínio da questão anterior, só que agora quer saber coisas relacionadas a energia armazenada.
A questão quer que o aluno mostre que o resistor tem uma certa equação, e em seguida comparar com o resultado da questão anterior.
Essa questão é interessante, uma vez que se pode escolher qual configuração pode ser usada