Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 7.Problemas - Ex. 14
Calcule a constante de tempo do circuito na figura 7.94.
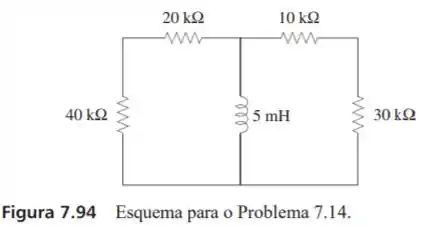
Passo 1
Para um circuito a constante de tempo é dada por
Precisamos então calcular a resistência equivalente que vai ser dada por
Portanto, a constante de tempo vai ser dada por
Resposta
Exercícios de Livros Relacionados
Obtenha v(t) e i(t) no circuito da Figura 7.128.
A resistência de uma bobina de 160m H é igual a 8Ω . Determine o tempo necessário para a corrente chegar a 60 % de seu valor final quando a tensão é aplicada à bobina.
A chave da Figura 7.142 passa da posição a para a posição b em t = 0. Use o PSpice ou MultiSim para determinar i(t) para t0.
No circuito da Figura 7.144, supondo que a chave já se encontre na posição a por um longo período, determine: i 1 0 ,i 2 0ev 0 ( 0 ) i L ( t ) i 1 ∞ ,i 2 ∞ev 0 ( ∞ )
No circuito da Figura 7.143, a chave já se encontra na posição a há um bom tempo, porém, muda de repente para a posição b em t = 0. Determine i 0 (t).