Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 7.Problemas - Ex. 64
Determine (t) e a energia total dissipada pelo circuito a seguir de t = 0 a t = s. O valor de (t) é igual a [40– 40u(t)] V.
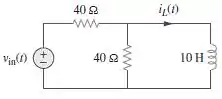
Passo 1
Este problema pode ser resolvido por diferentes maneiras, mas vamos utilizar por Thevenin, ou seja, encontrar o circuito equivalente composto por uma fonte de tensão e um resistor em série.
De tal modo que o circuito resultante seja,
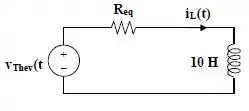
Passo 2
Certo! O primeiro passo é tirar o indutor do circuito e deixar aberto.
Para encontrarmos a resistência de Thevenin, devemos dar curto na fonte de tensão e tirar o paralelo dos dois resistores, assim
E como o circuito está aberto no indutor a tensão entre os pontos do resistor de pode ser calculado por divisor de tensão. Como os dois resistores são iguais, temos:
Passo 3
Pronto! Agora que encontramos o circuito equivalente podemos resolver do mesmo jeito que as questões anteriores. Primeiro vamos encontrar a constante de tempo,
Para t
Observe que,
Assim,
Para t>0:
Note que,
Assim,
Substituindo em,
Temos
Passo 4
A energia dissipada é dada por: