Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 7.Problemas - Ex. 11
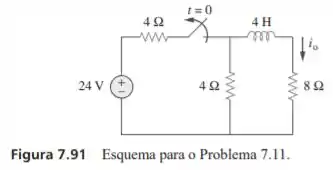
Para o circuito da figura 7.91, determine para .
Passo 1
Analisando as informações presentes no circuito dado no exercício, podemos perceber que para o circuito está “completinho” e assim, poderemos encontrar através de um divisor de corrente. Primeiramente devemos ver que os resistores de estão em paralelo e calculando sua resistência equivalente vamos achar , continuando o processo e aplicando o divisor de corrente encontraremos
Agora, se analisarmos para é possível perceber que temos um circuito sem fonte e então, nossa constante de tempo será dada por
Portanto, nosso para pode ser equacionado como
Resposta
Exercícios de Livros Relacionados
A resistência de uma bobina de 160m H é igual a 8Ω . Determine o tempo necessário para a corrente chegar a 60 % de seu valor final quando a tensão é aplicada à bobina.
A chave da Figura 7.142 passa da posição a para a posição b em t = 0. Use o PSpice ou MultiSim para determinar i(t) para t0.
No circuito da Figura 7.144, supondo que a chave já se encontre na posição a por um longo período, determine: i 1 0 ,i 2 0ev 0 ( 0 ) i L ( t ) i 1 ∞ ,i 2 ∞ev 0 ( ∞ )
No circuito da Figura 7.143, a chave já se encontra na posição a há um bom tempo, porém, muda de repente para a posição b em t = 0. Determine i 0 (t).
Um gerador CC de 120V energiza um motor cuja bobina possui indutância de 50H e resistência de 100Ω . Um resistor de descarga de campo de 400Ω é ligado em paralelo com o motor para evitar dano a esse ú