Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 7.Problemas - Ex. 8
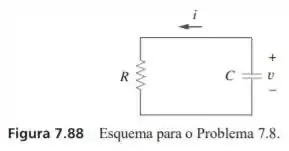
Para o circuito da figura 7.88, se
Determine e .
Determine a constante de tempo.
Calcule a energia inicial no capacitor.
Obtenha o tempo necessário para dissipar da energia inicial.
Passo 1
Para encontrarmos os valores de vamos utilizar a seguinte ideia: como temos o valor de e podemos aplicar a lei de Ohm e encontraremos, assim, o valor de . Então,
Agora que temos o valor de podemos encontrar o valor de facilmente haja vista que a constante de tempo foi dada de forma implícita no enunciado e seu valor é . Então, como para um circuito temos que
Passo 2
Para calcularmos a energia inicial no capacitor teremos que aplicar a seguinte equação
Por fim, para encontrarmos o tempo necessário para dissipar da energia inicial façamos o seguinte
Resposta
Exercícios de Livros Relacionados
Qual porcentagem da energia inicial armazenada no capacitor da Figura 7.23 é dissipada pelo resistor de 40 kV?
A chave no circuito da Figura P7.25 esteve na posição a por um longo tempo e v2 = 0 V. Em t = 0, a chave é colocada na posição b. Calcule a) i, v1 e v2 para t $ 0+, b) a energia armazenada no capacito
No circuito mostrado na Figura P7.26, ambas as chaves funcionam em conjunto; isto é, abrem- -se ou fecham-se ao mesmo tempo. Elas estiveram fechadas por um longo tempo antes de se abrirem em t = 0. a)
A chave no circuito da Figura P7.27 é fechada em t = 0, após permanecer aberta por um longo tempo. a) Determine i 1 (0-) e i 2 (0-). b) Determine i 1 (0+) e i 2 (0+). c) Explique por que i 1 (0-) = i
No circuito da Figura P7.29 as expressões paraa tensão e a corrente sãov = 72e-500t V, t $ 0;i = 9e-500t mA, t $ 0+.Determinea) R.b) C.c) t (em milissegundos).d) A energia inicial armazenada no capaci