Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 7.Problemas - Ex. 27

A chave no circuito da Figura P7.27 é fechada em t = 0, após permanecer aberta por um longo tempo. a) Determine i 1 (0-) e i 2 (0-). b) Determine i 1 (0+) e i 2 (0+). c) Explique por que i 1 (0-) = i 1 (0+). d) Explique por que i 2 (0-) ≠ i 2 (0+). e) Determine i 1 (t) para t $ 0. f) Determine i 2 (t) para t $ 0+.

Passo 1

[a] - t < 0 : O circuito depois de muito tempo o capacitor fica estável e passa a ser inutilizado no circuito, para facilitar a visualização, é bom fazer uma conversão na fonte de corrente que está em paralelo com o resistor de 20   Ω , então temos:

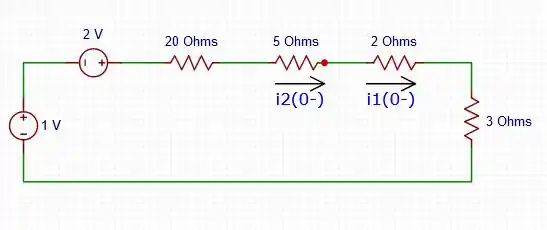
E com isso, podemos ter o cálculo de i 1 ( 0 - ) e i 2 0 - , elas passam pelo mesmo ponto do circuito, por assim dizer, então:

i 1 0 - = i 2 0 - = 3 30 = 100   m A

Passo 2

[b] – t > 0 : Agora a chave está fechada, e o circuito muda a configuração, e com isso, os valores das correntes não são mais os mesmos, a corrente i 2 ( 0 + ) “percorre” um caminho maior vamos assim dizer, então:

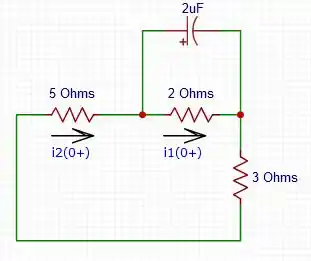
Para i 1 ( 0 + ) :

i 1 0 + = 0,2 2 = 100   m A

E para i 2 ( 0 + ) :

i 2 0 + =   - 0,2 8 =   - 25   m A

Passo 3

[c] – O capacitor não pode mudar sua tensão instantaneamente, por isso:

i 1 0 - = i 1 0 + = 100   m A

Passo 4

[d] – A troca de polaridade pode causar uma mudança instantânea na corrente no ramo resistivo. Neste circuito quem sofre com esse efeito é a corrente i 2 .

i 2 0 - = 100   m A     e     i 2 0 + = - 25   m A

Passo 5

[e] – Para o cálculo de v c , obtemos a seguinte configuração:

v c = 0,2 e - t / τ ,     t ≥ 0  

Com isso, tem que calcular a constante de tempo, que é igual a:

τ = R e C = 1,6 2 × 10 - 6 = 3,2   μ s ;

E sua inversa:

1 τ = 312500

Com isso, temos:

v c = 0,2 e - 312500 t   V ,     t ≥ 0  

A corrente i 1 é somente v c dividido por 2 (que é o valor do resistor), logo

i 1 = v c 2 = 0,1 e 312500 t   A ,     t ≥ 0

Passo 6

[f] – Para i 2 , o raciocínio é análogo, com o adendo do sentido de a tensão ser invertida e ter uma combinação de resistores.

i 2 =   - v c 8 = - 25 e 312500 t   m A ,     t ≥ 0 +

Resposta

a )   i 1 0 - = i 2 0 - = 100   m A

b )   i 1 0 + = 100   m A   e   i 2 0 + =   - 25   m A  

c )   i 1 0 - = i 1 0 + = 100   m A

d )   A   t r o c a   d e   p o l a r i d a d e   p o d e   c a u s a r   u m a   m u d a n ç a   i n s t a n t â n e a   n a   c o r r e n t e   n o   r a m o   r e s i s t i v o .

e ) i 1 = v c 2 = 0,1 e 312500 t   A ,     t ≥ 0

f )   i 2 =   - v c 8 = - 25 e 312500 t   m A ,     t ≥ 0 +    

Exercícios de Livros Relacionados

Mostre que x = x 1 + x 2 = A 1 e - 2 t + A 2 e - 3 t Também é uma solução da equação diferencial do Ex. 9.2.1
Mostre que x 1 = A 1 e - 2 t e x 2 = A 2 e - 3 t são soluções de d 2 x d t 2 + 5 d x d t + 6 x = 0 Independentemente do valor das constantes A 1 e A 2 .
Mostre que se o membro da direita da equação diferencial do Ex. 9.2.1 é alterado de 0 para 12 , então x = A 1 e - 2 t + A 2 e - 3 t + 2 É uma solução. Então a resposta natural é A 1 e - 2 t + A 2 e -
Dado(a) d 2 x d t 2 + 7 d x d t + 10 x = 0 (b) d 2 x d t 2 + 4 d x d t + 4 x = 0 Calcule a equação característica e as frequências naturais em cada caso.
Dada a equação diferencial não-linear x d 2 x d t 2 - t d x d t = 0 Mostre que x 1 = t 2 e x 2 = 1 são soluções mas x 1 + x 2 não é uma solução.