Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas - Ex. 17
No circuito da Figura 8.71, a chave se move instantaneamente da posição para em . Determine para qualquer .
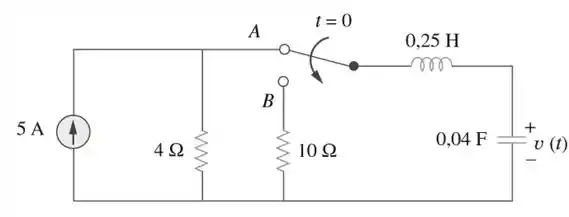
Passo 1
Relaxa, galera. Vamo se Ligar e achar a Resposta. Primeiro vamos definir algumas coisas do circuito, usando as infos que temos dele! Vamos lá! Do circuito, temos que,
Passo 2
Continuando, temos que:
O que nos leva a,
Logo,
Temos:
Resposta
Exercícios de Livros Relacionados
Considere o circuito RLC em paralelo da Figura 8.60. Que tipo de resposta ele produzirá?(a) com amortecimento supercrítico(b) com subamortecimento(c) com amortecimento crítico(d) nenhuma das alternati
Um circuito RLC em paralelo possui L = 2 H e C = 0,25 F. O valor de R que produzirá um fator de amortecimento unitário é:(a) 0,5 Ω (b) 1 Ω (c) 2 Ω (d) 4 Ω
Consulte o circuito RLC na Figura 8.59. Que tipo de resposta ela produzirá?(a) com amortecimento supercrítico(b) com subamortecimento(c) com amortecimento crítico(d) nenhuma das alternativas anteriore
Se as raízes da equação característica de um circuito RLC forem –2 e –3, a resposta é:(a) ( Ac o s2 t+Bs e n2 t ) e - 3 t (b) A+ 2 B t e - 3 t (c) A e - 2 t + B t e - 3 t (d) A e - 2 t + B e - 3 t ond
Um circuito RLC em série possui R = 20 k Ω , L = 0,2 mH e C = 5 μ F. Que tipo de amortecimento é apresentado pelo circuito?