Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Questões para revisão - Ex. 4

Se as raízes da equação característica de um circuito RLC forem –2 e –3, a resposta é:

(a) ( A   c o s   2 t   +   B   s e n   2 t ) e - 3 t

(b) A   + 2 B t e - 3 t

(c) A e - 2 t + B t e - 3 t

(d) A e - 2 t + B e - 3 t

onde A e B são constantes.

Passo 1

Vamos lembrar o que é uma equação característica, vamos utilizar o circuito RLC abaixo como exemplo,

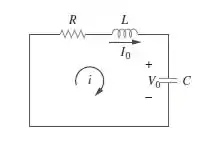
Se resolvermos as equações diferencias desse circuito encontraremos

s 2 + R L s + 1 L C = 0

A questão afirma que as raízes dessa equação é:

s 1 =   - 2

s 2 = - 3

Passo 2

Certo! Os dois valores de s indicam que há duas soluções possíveis para i, cada uma das quais na forma da solução

i = A e s t

Isto é:

i 1 = A 1 e s 1 t

i 2 = A 2 e s 2 t

Com são equações lineares, qualquer combinação das duas soluções distintas também é uma solução. Consequentemente, a resposta natural do circuito RLC em série é:

i t = A 1 e s 1 t + A 2 e s 2 t    

Passo 3

Assim, temos que a solução para a questão é:

A e - 2 t + B e - 3 t

Visto que os valores das raízes são -2 e -3 como mencionado no passo 1.

Resposta

Item d)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Obtenha um filtro passa-faixa ativo usando a configuração do Prob. 15.4 , com f 0 = 1000H z , Q = 10 e K = 2 , com capacitores de 0,01 μ F . (Sugestāo: Ver Prob. 15.10.)
Calcule i ,t0 , se v 0 = 6V e i 0 = 2A
Calcule i para t0 , se i g = 10A e o circuito está em regime permanente em t = 0 - .
A resistência no Problema 8.1 é reduzida para 80Ω . Determine a expressão para v(t) quando t ≥ 0 .
A resposta natural do circuito na Figura 8.1 é v t = 120 e - 400 t cos ⁡ 300 t + 80 e - 400 t sin ⁡ 300 tV , quando o capacitor é de 250 μ F . Determine (a) L; (b) R; (c) V 0 ; (d) I 0 e (e) i L ( t )