Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas - Ex. 14

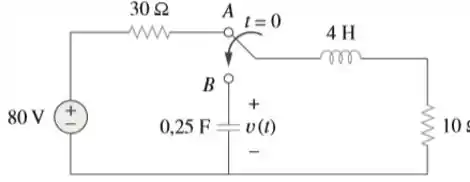
A chave na Figura 8.69 muda da posição A para a B em t   =   0 (observe atentamente que a chave deve se conectar ao ponto B antes de ela desfazer a conexão em A , um interruptor). Fazendo v ( 0 )   =   0 , determine v ( t ) para t >   0 .

Passo 1

Relaxa, galera. Vamo se Ligar e achar a Resposta. Vamos lá! Quando o interruptor está na posição A, v 0 - = 0 e i L 0 = 80 40 = 2 A . Quando o interruptor está na posição B, temos um circuito RLC sem fontes.

α = R 2 L = 10 2 × 4 = 1.25

ω 0 = 1 L C = 1 1 4 × 4 = 1

Passo 2

Sabendo que α > ω 0 , temos um caso de super amortecido!

s 1,2 = - α ± α 2 - ω 0 2 = - 1.25 ± 1.562

v t = A e - 2 t + B e - 0.5 t

v 0 = 0 = A + B

i C 0 = C d v 0 d t = - 2   o u d v 0 d t = - 2 C = - 8

Passo 3

Mas,

d v t d t = - 2 A e - 2 t - 0.5 B e - 0.5 t

Logo,

d v 0 d t = - 2 A - 0.5 B = 8

Resolvendo   v 0 = 0 = A + B e d v 0 d t = - 2 C = - 8

v t = 5.333 e - 2 t - 5.333 e - 0.5 t   V

Resposta

v t = 5.333 e - 2 t - 5.333 e - 0.5 t   V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para t0 no EX. 9.7 . 2 , calcule:a) v b) i
Calcule i , v , d i d ted v d t e mt = 0 + d x d t + 2 x + ∫ 0 t x d t = f ( t ) x 0 = - 1
Calcule a equação diferencial satisfeita por i no circuito,Use este resultado para calcular i para t0 , se R = 10 Ω ,L = 2 H ,C = 0,05 F ,v 0 = 0 e i 0 = 6 A .
Quanto maior o valor de R, menor o amortecimento que existirá no cabo de um circuito subamortecido paralelo RLC (porque α = 1 2 R C ) . Assuma R = ∞ (circuito aberto) e mostre que, no caso sem fontes,
Em um circuito RLC paralelo sem fontes, R = 1k ΩeC = 1μ F . Calcule L tal que o circuito seja:a) superamortecido com S 1,2 = - 250 , - 750s - 1 ; b) superamortecido com w d = 250 r a d s ; c) com amor