Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas - Ex. 21

Calcule v ( t ) para t > 0 no circuito da Figura 8.75.

Passo 1

Relaxa, galera. Vamo se Ligar e achar a Resposta. Combinando os resistores, temos que:

60 | | (15 + 25) = 24 omega

Tornando o circuito assim:

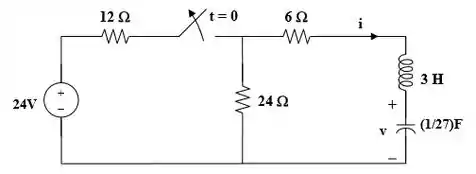
Em t = 0 - , i (0) = 0 , v (0) = 24 xx (24)/(36) = 16 V

Passo 2

Para t > 0 , temos um R L C . R = 30 omega , L = 3 H , C = ( 1 // 27 ) F . E isso é bom, porque daqui basta a gente achar as constantes que definem v ( t ) !

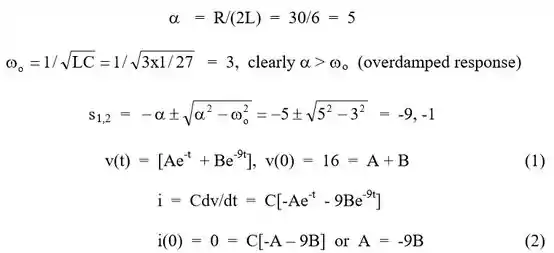
De ( 1 ) e ( 2 ) , temos que:

B = - 2 e A = 18 .

Logo,

v (t) = (18 e^(- t) - 2 e^(- 9 t)) V

Resposta

v (t) = (18 e^(- t) - 2 e^(- 9 t)) V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A chave na Figura 8.69 muda da posição A para a B em t=0 (observe atentamente que a chave deve se conectar ao ponto B antes de ela desfazer a conexão em A , um interruptor). Fazendo v ( 0 )=0 , determ
As respostas de um circuito RLC em série são v C t = 30 - 10 e - 20 t + 30 e - 10 tV i L t = 40 e - 20 t - 60 e - 10 tm A Onde v C e i L são, respectivamente, a tensão no capacitor e a corrente no ind
Para o circuito da Figura 8.68, calcule o valor de R necessário para se obter uma resposta com amortecimento crítico.
Determine i ( t ) para t0 no circuito da Figura 8.70.
A chave do circuito da Figura 8.74 já se encontra fechada há um longo tempo, porém é aberta em t=0 . Determine i ( t ) para t0 .