Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas - Ex. 52
52- Se no circuito da Figura , determine .
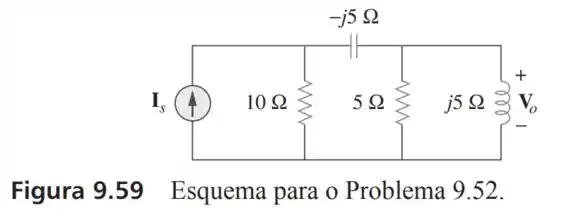
Passo 1
Como sabemos a tensão na reatância de e na resistência de então temos que a tensão encontra-se em cima da impedância de:
Agora vamos transformar a fonte de corrente em uma fonte de tensão igual a:
Nos dando o seguinte circuito:
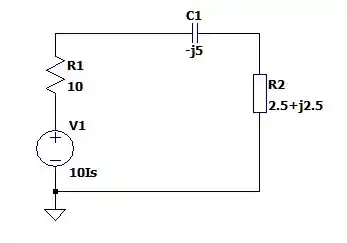
A corrente total que passa por esse circuito é de igual a:
Passo 2
Dessa forma o valor de será:
Resposta
Exercícios de Livros Relacionados
Calcule a condutância e a susceptância, se Z é (a) 3 + j 4 , (b) 0,4 + j 0,3 e (c) 2 2 ∠ 45 °
Calcule a admitância vista pelos terminais da fonte na Fig. 10.4, nas formas retangular e polar.
Calcule a resposta forçada i, na Fig. 10.4, se L = 8mH, R =12 k Ω , V m = 5V, e ω = 2 * 10 6 rad/s.
Calcule o valor em regime permanente de i , se (a) w = 1r a d / s e (b) 2r a d / s . Note que, no último caso, a impedância vista pelos terminais da fonte é puramente resistiva.
Calcule a impedância do circuito da Fig. 10.15, se as funções no domínio do tempo representadas pelos fasores V e I são(a) v = - 30 cos 2 t + 16 sin 2 tV , i = 1,7 cos 2 t + 20 °A .(b) v = R e j