Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas - Ex. 49
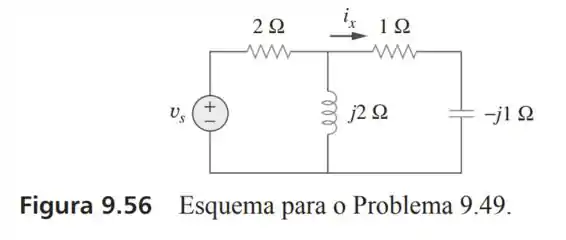
49- Determine no circuito da Figura se a corrente no resistor de for .
Passo 1
O fasor da corrente dada no enunciado é de:
E vamos olhar para o circuito abaixo:
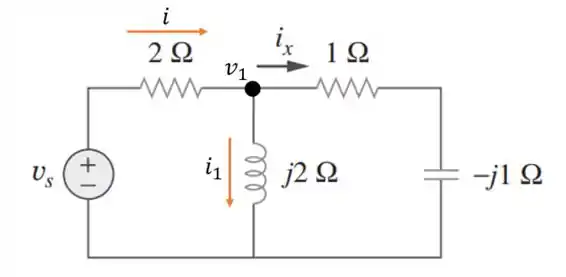
Vamos chamar de a tensão intermediária , e que pela lei de Ohm para impedância vale:
Ou seja:
Fazendo o fasor da impedância nós temos:
Passo 2
Agora podemos encontrar fazendo a somatória das correntes que entram e saem no nó de tensão igual a ou seja:
E substituindo por nós temos:
Como nós temos:
Porém a quer a resposta em função de e não em função do fasor e para isso vamos utilizar a função seno com frequência angular de pois é com essa frequência angular no qual todo o circuito funciona:
Então:
Resposta
Exercícios de Livros Relacionados
10.32. Calcule os valores v e v1 em regime permanente.
Desenhe o diagrama de polos e zeros da função de rede do Ex. 14.5.1
Se a equação representativa de um circuito é d 2 v o d t 2 + 4 ⋅ d v o d t + 13 v o = 2 ⋅ d v i d t + 4 v i Calcule H(s) e os polos e zeros.
Se os zeros de H(s) são s = - 1 , - 1 ± j 1 , os pólos são s = - 2 , - 1 ± j 2 e H 0 = 4 , calcule (s).
Mostre que os parâmetros y podem ser obtidos a partir dos parâmetros z por onde Δ z = Z 11 Z 22 - Z 12 Z 21 . (Isso e dado na primeira coluna da segunda linha da Tabela 14.1.) Use esse resultado para