Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas - Ex. 51
51- Se a tensão no resistor de no circuito da Figura for , obtenha :
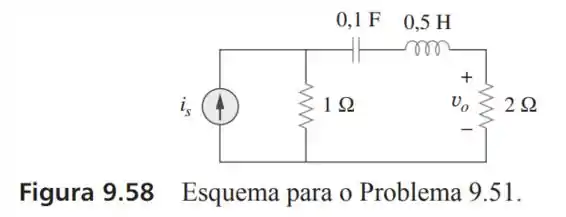
Passo 1
A reatância no capacitor e no indutor será:
E a corrente que passa pelo resistor de será:
O raciocínio é que a corrente que passa tem a mesma proporção que a outra reatância (na qual a corrente não passa dividido sobre a reatância da soma das duas (igual ao que se faz no circuito contínuo)
Passo 2
E como foi dado a tensão no resistor e sabendo que o fasor dessa tensão é então:
Em função de essa corrente será:
Resposta
Exercícios de Livros Relacionados
10.24. Calcule C tal que a impedância vista pela fonte seja real. Neste caso, calcule a potência absorvida pelo resistor de 12-Ω.
10.33. Calcule o valor de i em regime permanente quando (a) w = 1 rad/s, (b) w = 2 rad/s e (c)w = 4 rad/s (note que (b) é o caso com ressonância).
10.28. Calcule o valor da tensão v em regime permanente.
10.27. Calcule o valor da corrente i em regime permanente.
10.35. Calcule a corrente i em regime permanente.