Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas - Ex. 62
62- Para o circuito da Figura , determine a impedância de entrada a .
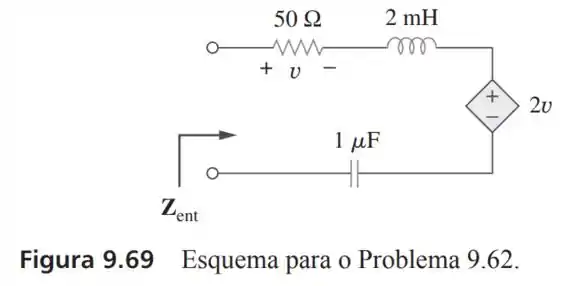
Passo 1
A reatância no indutor e no capacitor serão iguais a:
Passo 2
E para encontrar a resistência equivalente desse circuito (com fonte dependente) nós vamos fazer o mesmo que fizemos com o teorema de Thévenin em corrente contínua, que é colocar uma fonte de corrente de para caso tenhamos uma fonte de tensão dependente, da seguinte forma.
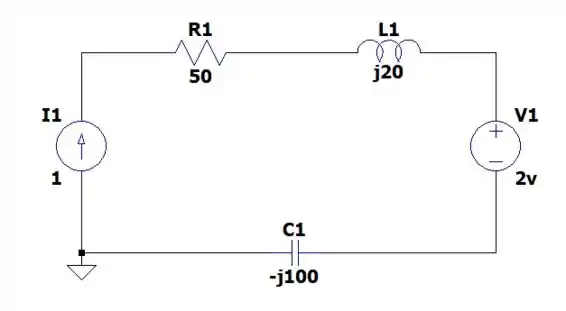
Dessa forma a corrente que rola em todo o circuito será de , fazendo com que seja:
E a somatória das tensões nesse circuito será para a tensão na fonte de corrente sendo igual a :
E como a corrente é de então a impedância entre os contatos da fonte será:
E essa impedância é a impedância de entrada.
Resposta
Exercícios de Livros Relacionados
a) Mostre que, a uma dada frequência v, os circuitos na Figura P9.18(a) e (b) terão a mesma impedância entre os terminais a,b se R 1 = ω 2 L 2 2 R 2 R 2 2 + ω 2 L 2 2 , L 1 = L 2 2 R 2 R 2 + ω 2 L 2 2
Calcule a função de rede Z(s) com uma entrada de soldagem através do resistor de 6 Ω da Figura 14.9 e use o resultado para encontrar as frequências naturais.
Verifique que 0 circuito da Fig. 14.22 e equivalente a rede genérica de três terminais, mostrando que (14.41) se aplica.
Mostre que o circuito e um filtro passa-faixa, com w 0 = 1 r a d s e altere em escala a frequência e a impedância para obter uma frequência central de 1000 r a d s , usando capacitores de 1μ Fe4 μ F .
Se H s = V 2 V 1 , no circuito do problema 15.1eL = 1H , calcule ReC de forma que o pico da amplitude ocorra em w = 10 r a d s e H j 6 = 0,707 .