Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas - Ex. 57
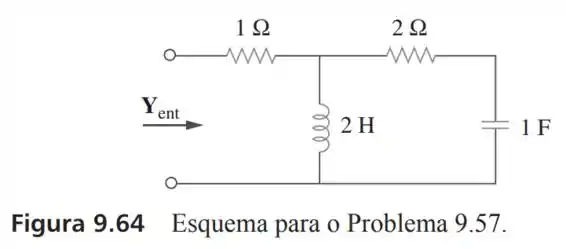
57- Com , obtenha a impedância de entrada do circuito da Figura
Passo 1
A reatância no capacitor e no indutor para essa valor de será igual a:
Passo 2
Dessa forma conseguimo que o indutor de está em paralelo com a série entre o resistor de e o capacitor de , os dando uma impedância equivalente a:
Multiplicando por em cima e embaixo teremos:
Essa impedância estará somada com a ressitência de nos dando então uma impedância total igual a:
Passo 3
Aí vem uma coisa meio estranha, a questão fala que quer a impedância de entrada , mas na imagem está que seria a susceptância de entrada, bem se for que ele quer então:
Multiplicando por teremos:
Resposta
Exercícios de Livros Relacionados
Calcule o valor em regime permanente de i , se (a) w = 1r a d / s e (b) 2r a d / s . Note que, no último caso, a impedância vista pelos terminais da fonte é puramente resistiva.
Um circuito tem uma imepedância Z = 4 1 + j ω 4 + j ω j ω 2 + j ωΩ Calcule a resistência, a reatância, a condutância e a susceptância com ω = 2r a d / s . Se a tensão no domínio do tempo aplicada ao c
Mostre que a função de transferência V 2 / V 1 é dada por: H s = V 2 s V 1 s = 1 R 1 s s 2 + 1 R 2 s + 1 R 3
Mostre que, no Prob. 15.6, se L = Q , C = 1 / Q e R = 1 , então H s = 1 Q s s 2 + 1 Q s + 1 Que é uma função de rede passa-faixa com índice de mérito Q , frequência central ω 0 = 1 rad/s, largura de f
Para o circuito mostrado, R = 2 Ω , L = 2H e C = 0.02F . Se a entrada e a saída forem V 1 e V 2 , respectivamente, calcule a função de rede e esboce as respostas em amplitude e fase. Mostre que o pico