Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 9.Problemas - Ex. 18

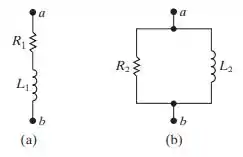
a) Mostre que, a uma dada frequência v, os circuitos na Figura P9.18(a) e (b) terão a mesma impedância entre os terminais a,b se

R 1 = ω 2 L 2 2 R 2 R 2 2 + ω 2 L 2 2 ,     L 1 = L 2 2 R 2 R 2 + ω 2 L 2 2

b) Determine os valores de resistência e indutância que, quando ligados em série, terão a mesma impedância a uma frequência de 4 krad/s que a de uma conexão em paralelo de um resistor de 5 kV e de um indutor de 1,25 H.

Passo 1

Saaaalve galerinha. Tudo bem com vocês? Então bora lá. Começando no item a),

Z 1 = R 1 + j ω L 1

Z 2 = R 2 ( j ω L 2 ) R 2 + j ω L 2 = ω 2 L 2 2 R 2 + j ω L 2 2 R 2 R 2 2 + ω 2 L 2 2

Z 1 = Z 2

Onde,

R 1 = ω 2 L 2 2 R 2 R 2 2 + ω 2 L 2 2 ,     L 1 = R 2 2 L 2 R 2 2 + ω 2 L 2 2

Passo 2

No item b),

R 1 = 4000 2 1.25 2 ( 5000 ) 5000 2 + 4000 2 1.25 2 = 2500   Ω

L 1 = 5000 2 ( 1.25 ) 5000 2 + 4000 2 1.25 2 = 625   m H

Resposta

R e s p o s t a   n o s   p a s s o s

Exercícios de Livros Relacionados

Para o circuito R L C em serie com uma fonte de tensão v g , faça a função de rede ser H=I / V g , ondeI e a corrente fasorial. Mostre que as respostas em amplitude e fase são similares as da Fig. 15.
Faça R=4 Ω , L=1 / 10H e C=1 / 40F na Fig. 15.1 e calcule a amplitude máxima e o ponto onde ela ocorre. Esboce também as respostas em amplitude e fase.
Com o uso da Tabela 14.1, calcule as condições de (a) os parâmetros h (b) os parâmetros de transmissão, para esse circuito ser recíproco ( Z 12 = Z 21 ) .
Um segundo conjunto de parâmetros de transmissão pode ser definido. exprimindo as variáveis de saída em termos das variáveis de entrada, por V 2 = a V 1 - b I 1 I 2 = c V 1 - d I 1 Calcule os parametr
Demonstre que o circuito dado e equivalente a rede reciproca genérica de três terminais, mostrando que (14.38) se aplica.