Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas - Ex. 60
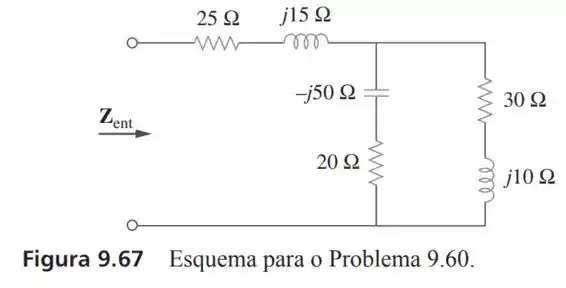
60- Obtenha para o circuito da Figura
Passo 1
Inicalmente vamos fazer a impedância equivalente entre as duas cargas em paralelo:
Pelo bem da simplicidade vamos transformar em fasor esses números complexos.
Passo 2
E agora podemos somar essa impedância equivalente com e que vai nos dar:
Resposta
Exercícios de Livros Relacionados
Faça R=4 Ω , L=1 / 10H e C=1 / 40F na Fig. 15.1 e calcule a amplitude máxima e o ponto onde ela ocorre. Esboce também as respostas em amplitude e fase.
Com o uso da Tabela 14.1, calcule as condições de (a) os parâmetros h (b) os parâmetros de transmissão, para esse circuito ser recíproco ( Z 12 = Z 21 ) .
Um segundo conjunto de parâmetros de transmissão pode ser definido. exprimindo as variáveis de saída em termos das variáveis de entrada, por V 2 = a V 1 - b I 1 I 2 = c V 1 - d I 1 Calcule os parametr
Demonstre que o circuito dado e equivalente a rede reciproca genérica de três terminais, mostrando que (14.38) se aplica.
Demonstre que o circuito dado é equivalente ao quadripolo genérico.